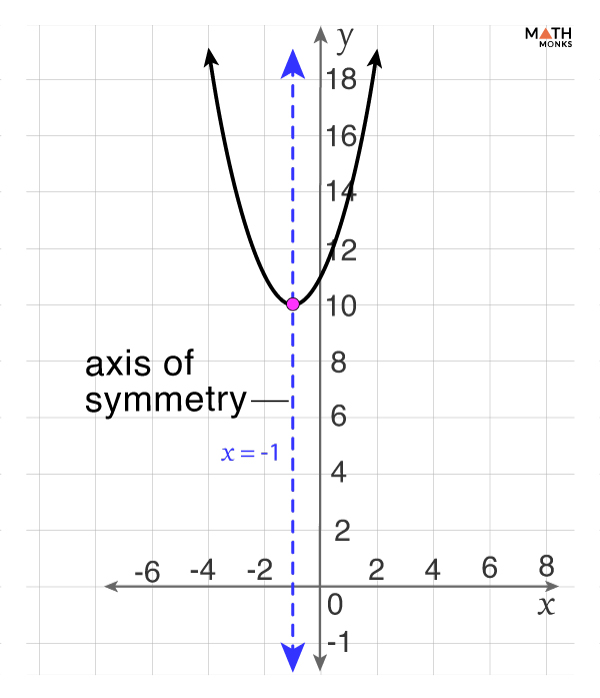
Does a seemingly simple curve hold the key to unlocking complex mathematical concepts? The axis of symmetry, a fundamental element of parabolas, plays a vital role in understanding the behavior and properties of quadratic functions.
At its core, the axis of symmetry acts as a mirror line, slicing a symmetrical shape into two identical halves. Consider a parabola, the familiar U-shaped curve often encountered in algebra. The axis of symmetry, in this context, is the vertical line that neatly bisects the parabola, passing directly through its vertex, the point where the curve changes direction.
The concept extends beyond parabolas; symmetrical shapes like ellipses and hyperbolas also possess axes of symmetry. A symmetry calculator can be a handy tool to identify these lines for various shapes, making it easier to visualize and analyze their properties. The equation of the axis of symmetry varies depending on the orientation of the parabola. For a parabola opening upwards or downwards, the equation is a simple vertical line, x = h, where (h, k) represents the vertex coordinates. Conversely, a parabola opening to the left or right has an axis of symmetry defined by the equation y = k.
- Desi Fry99com The Ultimate Guide To A Rising Star In The Digital World
- Filmyflyfi Your Ultimate Movie Streaming Hub
Understanding the axis of symmetry is particularly useful when working with quadratic functions expressed in the standard form: y = ax + bx + c. In this form, the axis of symmetry can be readily determined using the formula x = -b / 2a. This formula allows for the rapid identification of the axis of symmetry using only the coefficients 'a' and 'b' from the quadratic equation. This contrasts with the vertex form of a parabola, y = a(x - h) + k, from which the axis of symmetry (x = h) is immediately apparent. Both forms provide valuable insights into the nature of the parabola.
Let's delve deeper into the specifics of calculating the axis of symmetry. For a quadratic function in the standard form y = ax + bx + c, identifying the axis of symmetry involves a straightforward application of the formula x = -b / 2a. Here, 'a' is the coefficient of the x term, and 'b' is the coefficient of the x term. This formula directly provides the x-coordinate of the vertex and, consequently, the equation of the axis of symmetry.
The standard equation of a horizontal parabola is x = ay + by + c, where a, b, and c are real numbers and 'a' does not equal zero. The equation of the axis of symmetry in this case is y = -b / 2a. To find the values of a, b, and c, one can compare the given equation with x = ay + by + c. This is critical in finding the axis of symmetry.
- The Khatrimaza Your Ultimate Movie Experience Hub
- Emma Kenny Naked The Truth Behind The Clickbait And Misinformation
The axis of symmetry is especially helpful when graphing quadratic functions. It is a vertical line that runs through the vertex of the parabola. Therefore, it is a cornerstone concept in mathematics and geometry, dividing figures and equations into perfectly mirrored halves. For example, let's say we have the equation y = x - 6x + 8. First, identify the coefficients: a = 1, b = -6, and c = 8. Then, apply the formula: x = -(-6) / (2 1) = 3. Thus, the axis of symmetry for this parabola is the vertical line x = 3. You can verify this by completing the square to rewrite the equation in vertex form, which will directly reveal the vertex's x-coordinate.
The vertex, where the parabola changes direction, lies on the axis of symmetry. The axis of symmetry is the line that passes through the vertex and is perpendicular to the directrix, another important element in defining a parabola. Understanding the relationship between the vertex, axis of symmetry, and directrix provides a comprehensive view of a parabola's structure.
For instance, consider a parabola with the equation y = x - 4x + 3. To find its axis of symmetry, we can use the formula x = -b / 2a. Here, a = 1 and b = -4. Therefore, x = -(-4) / (2 1) = 2. This means the axis of symmetry is the vertical line x = 2. The vertex form of this equation is y = (x - 2) - 1, confirming that the vertex is at the point (2, -1), which indeed lies on the line x = 2.
The concept of symmetry extends beyond parabolas. Symmetry is a fundamental concept in many fields, including art, design, and even nature. Identifying lines of symmetry helps us better understand the balance, harmony, and aesthetic appeal of objects and structures. The axis of symmetry serves as a foundational concept when working with quadratic functions, offering a powerful tool for analyzing and graphing parabolas.
Therefore, to find the axis of symmetry for a quadratic function in the form y = ax + bx + c, employing the equation x = -b / 2a is key. The application of this equation is widespread and ensures accurate calculation of the axis of symmetry. The value 'a' and 'b' are essential for identifying the axis of symmetry for any quadratic function, validating its accuracy for use in different quadratic equations.
The axis of symmetry equation is a vital mathematical formula used to pinpoint the location of the axis of symmetry within a given function. The axis of symmetry is the line that divides a function into two mirror image halves.
Rewriting a quadratic equation into vertex form, y = a(x - h) + k, is another means to identify the axis of symmetry, as the x-coordinate of the vertex, h, directly corresponds to the axis of symmetry (x = h). This provides an alternative method to visualize and calculate the line of symmetry.
The formula x = -b / 2a provides the x-coordinate of the vertex, and the line x = -b / 2a defines the axis of symmetry. The axis of symmetry is the vertical line that passes through the vertex of the parabola.
Let's look at an example: Y = x - 4x + 3. First identify the values of a, b, and c. a = 1, b = -4, and c = 3. To find the axis of symmetry, plug these numbers into the formula x = -b / 2a, which gives us x = -(-4) / (2 * 1) = 2. Therefore, the axis of symmetry is the vertical line x = 2. This line passes through the vertex of the parabola, which can be found by completing the square or using the vertex formula.
In conclusion, the axis of symmetry is a crucial concept in understanding and working with parabolas. It's the line that divides the parabola into two symmetrical halves, and its position can be calculated using a simple formula: x = -b / 2a, making it an indispensable tool for anyone studying algebra or graphing quadratic functions. Learning how to find the equation of the axis of symmetry of a parabola from its graph or equation is a useful skill.
Here's a table summarizing key aspects of the axis of symmetry:
| Aspect | Description |
|---|---|
| Definition | A line that divides a symmetrical shape (like a parabola) into two congruent parts. |
| For Parabolas | The vertical line that passes through the vertex of the parabola. |
| Equation (Standard Form y = ax + bx + c) | x = -b / 2a |
| Equation (Vertex Form y = a(x - h) + k) | x = h (where (h, k) is the vertex) |
| Significance | Helps in understanding the symmetry and properties of the parabola, and aids in graphing. |
| Relationship to Vertex | The axis of symmetry always passes through the vertex. |
- Golden Somali Vip Telegram Your Ultimate Guide To Unlocking Exclusive Insights
- Sky Movies Hd In Your Ultimate Guide To Unmatched Entertainment