Are you ready to unlock the hidden language of mathematics and visualize the complex relationships that govern our world? Mathematics, often perceived as an abstract and daunting subject, becomes remarkably accessible and engaging when we harness the power of graphing tools.
From the simplest linear equations to the most intricate calculus problems, graphing provides a visual representation that transforms abstract concepts into tangible realities. By plotting points, visualizing functions, and exploring algebraic equations, we can gain a deeper understanding of mathematical principles and their applications in diverse fields.
Let's delve into the fascinating world of graphing and discover how it can revolutionize our approach to mathematics.
- Sky Movie Hd Your Ultimate Guide To Streaming Highdefinition Movies
- The Khatrimaza Your Ultimate Movie Experience Hub
| Topic | Details |
|---|---|
| What is Graphing? | Graphing is the visual representation of mathematical relationships using a coordinate plane. It allows us to plot points, visualize functions, and explore algebraic equations. |
| Key Components | A point and a coordinate plane |
| Types of Graphs |
|
| Coordinate Systems |
|
| Applications |
|
| Tools and Techniques |
|
| Benefits |
|
| Resources |
|
The world of mathematics is a vast and intricate landscape, often hidden behind a veil of abstract symbols and complex equations. However, when we employ the tools of graphing, this landscape transforms, revealing patterns, relationships, and insights that were once obscured. From the most elementary concepts to the most advanced theories, graphing provides a visual language that allows us to explore and understand the very essence of mathematics.
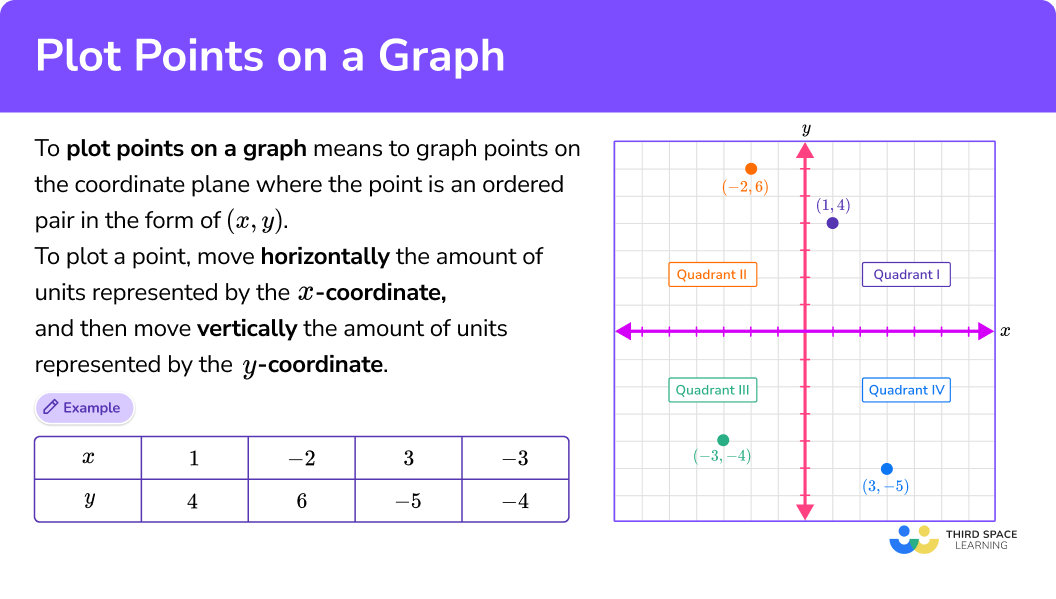
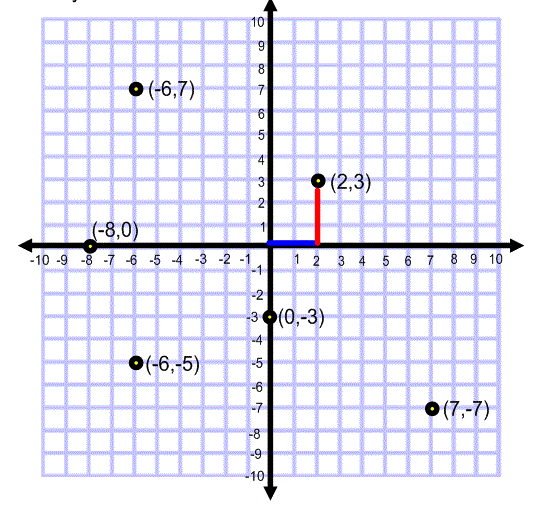
The fundamental building blocks of graphing are the point and the coordinate plane. A point, represented by a pair of coordinates (x, y), marks a specific location in space. The coordinate plane, with its x-axis (horizontal) and y-axis (vertical), provides the framework for locating these points and visualizing their relationships. Whether we are working with Cartesian coordinates or polar coordinates, the principle remains the same: to represent mathematical concepts visually.
Consider, for example, the simple act of plotting the points (1, 2) and (3, 4). By entering these coordinates into a graphing tool, we instantly see their positions on the plane. This seemingly simple exercise lays the foundation for more complex tasks, such as graphing lines, curves, and even three-dimensional objects. The ability to visualize these relationships is key to understanding their mathematical properties.
- Bollyflixcom Bollywood Your Ultimate Destination For Streaming Bollywood Movies
- Bollyflix Official Site Your Ultimate Guide To Bolly Flix
Graphing isn't just about plotting points; it's about understanding the underlying functions and equations that generate these points. For instance, the equation y = x + 4 defines a line. By choosing different values for 'x' (such as 3), we can calculate the corresponding 'y' value (7), and thus, identify the point (3, 7) on the graph. This process of translating equations into visual representations is a cornerstone of mathematical understanding.
Moreover, graphing tools allow us to explore complex functions, like quadratic equations (e.g., y = x + 2). By plotting the points generated by such equations, we can visualize their parabolic curves and understand their unique properties, such as the vertex, axis of symmetry, and intercepts. This visual representation goes beyond mere calculation; it allows us to appreciate the shape, form, and behavior of these mathematical entities.
Online graphing calculators and software, such as GeoGebra, provide a wealth of tools and features that enhance the graphing experience. With these tools, you can:
- Graph functions, data, and equations with ease.
- Add sliders to adjust parameters and observe the resulting changes in real-time.
- Animate graphs to visualize dynamic processes and transformations.
- Explore functions, curves, conics, and inequalities.
- View the coordinates of points and find key characteristics.
These interactive tools empower users to explore mathematical concepts in a dynamic and engaging way. They are not just calculators; they are powerful learning aids that transform abstract concepts into concrete visual experiences.
Graphing extends beyond simple equations. It is crucial for analyzing and interpreting data, identifying trends, and solving real-world problems. Consider the example of graphing a line represented by the equation 2x + 3y = 6. By using the origin (0, 0) as a test point, we can determine whether (0, 0) is a solution to the inequality 2x + 3y 6. This allows us to shade the appropriate region of the graph, visually representing the solution set.
Furthermore, graphing aids in visualizing and understanding concepts from calculus, such as slope fields for differential equations, and areas between curves. In geometry, graphing tools can create diagrams of polygons, helping to teach geometric courses.
To plot a point effectively, two elements are essential: the point itself, defined by its coordinates, and the coordinate plane, which provides the reference system. The process of plotting a point involves identifying its x and y coordinates, then following the gridlines until the two values meet and drawing a point at their intersection. If given a point (200, 300), one would locate 200 on the x-axis, and then 300 on the y-axis, and mark the point where these lines intersect.
Graphing offers a powerful lens through which to view the world. It makes mathematical concepts more accessible, enhances understanding, and improves problem-solving skills. Whether you are a student, educator, or simply someone curious about the world around you, embracing graphing tools is a valuable investment in your mathematical journey. Using these tools enables you to:
- Explore mathematical concepts in a dynamic and engaging way.
- Visualize complex relationships that are often difficult to grasp.
- Analyze and interpret data effectively.
- Solve problems in diverse fields, from science and engineering to economics.
- Unlock the hidden language of mathematics, making it more accessible and less intimidating.
By exploring math with graphing, you can transform abstract concepts into concrete, visual experiences, paving the way for a deeper understanding of the world.
With the right tools and a curious mind, anyone can harness the power of graphing to unlock the mysteries of mathematics and discover its beauty and utility. Try it today and see how graphing can transform your understanding of the world!
- Hdhub4u 18 Unveiling The World Of Premium Content
- Bollyflix World Your Ultimate Destination For Bollywood Entertainment
![How to do Calculations Using Points on a Graph [Video & Practice]](https://cdn-academy.pressidium.com/academy/wp-content/uploads/2021/01/point-a-plotted-at-23.png)