Can you unravel the mysteries of the mathematical world with a simple line? Linear equations, often overlooked, are the fundamental building blocks of understanding relationships and predicting outcomes in a variety of fields, from finance to physics.

The realm of mathematics offers a fascinating landscape where abstract concepts come to life. Within this world, linear equations stand out as both foundational and versatile. These equations, at their core, describe a straight line on a graph, a visual representation that provides insights into a multitude of real-world phenomena. But what exactly are these equations, and why are they so important?

A linear equation is, in essence, an equation with two variables that, when graphed, produces a straight line. The beauty of these equations lies in their simplicity and predictability. Unlike complex, nonlinear equations that might produce curves or erratic patterns, linear equations adhere to a consistent, predictable form. This consistency makes them incredibly useful for modeling and understanding a wide range of relationships. Consider the equation y = 1/4x + 5. In this context, the values in the equation do not need to be restricted to whole numbers. Here, the term 1/4, often denoted as 'm,' represents the slope of the line, while 5, or 'b,' signifies the y-intercept the point where the line crosses the y-axis.

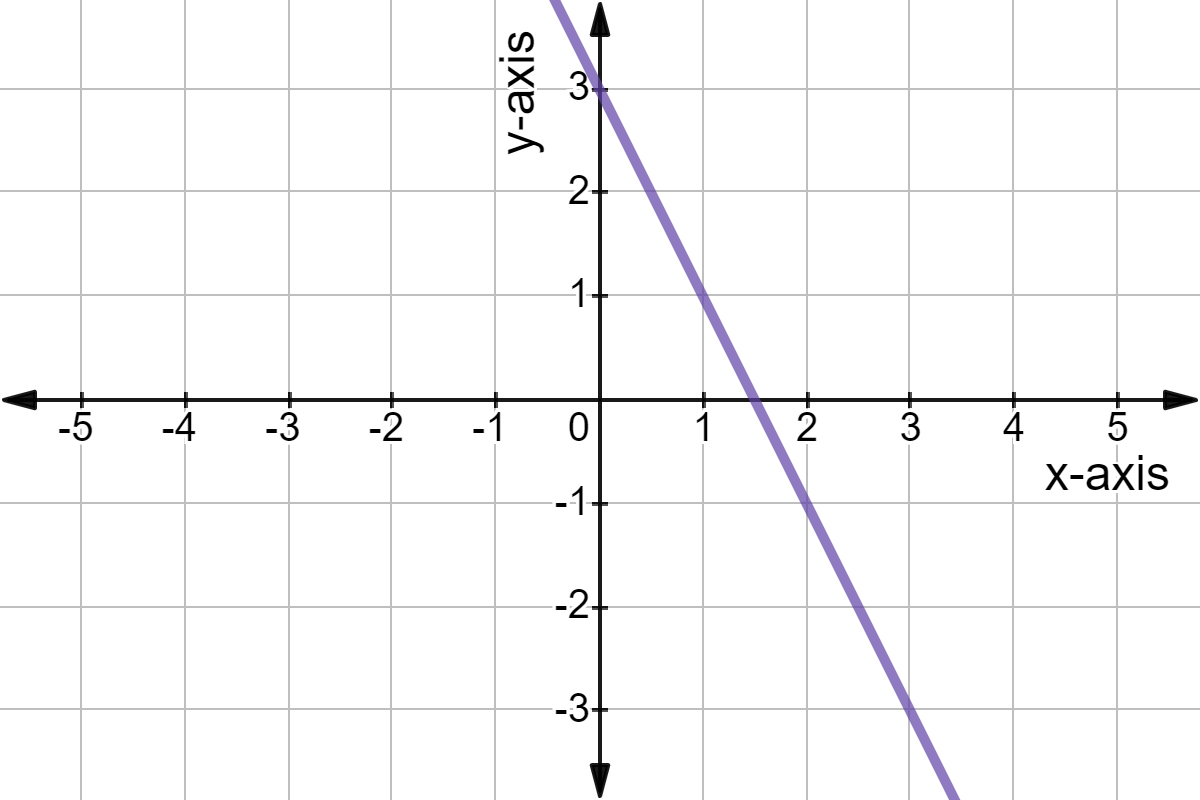
Let's delve deeper. Imagine the equation y = 2x + 1. The ability to graph this equation and understand its characteristics unlocks a deeper level of mathematical comprehension. Consider this: a linear equation, when graphed, will always present itself as a line. This simple fact is the core of understanding linear equations: it is a fundamental characteristic of their nature. To graph a linear equation, you can pinpoint any two points on the line, or apply alternative methods for a more streamlined approach. The world of linear functions is both elegant and practical.

To grasp the concept further, let's analyze how different forms of equations appear on the graph. Equations like y = -3x or even y = -3, when graphed in the same coordinate system, showcase distinct properties. The former equation, y = -3x, includes the variable 'x', demonstrating a variable relationship, and its representation is a diagonal line that descends as 'x' increases. Conversely, the latter, y = -3, shows no x-variable. Its solution produces a horizontal line crossing the y-axis at -3. Both equations, each unique in their construction, have their own characteristics. One reveals a fluctuating relationship with the variable; the other presents a constant value across x values. The significance here is not just in the equations' individual forms but in their collective visual behavior on a graph, which provides insight into their individual mathematical behaviors.

Let's explore the concept of nonlinear functions. For example, the function a = s2, which describes the area of a square, is non-linear because its points (1,1), (2,4), and (3,9) do not lie on a straight line. Unlike linear equations, these functions do not conform to a constant rate of change, resulting in curves or complex shapes on a graph. Recognizing this contrast is important.

The method for graphing can vary. For instance, we can substitute x = 0 in the equation to solve for y. We can also apply the concept of transformations. A function can be shifted upwards, downwards, left, or right. It might also be stretched, compressed, or even reflected. These transformations allow us to manipulate and visualize functions in various ways, offering a flexible approach to graphing linear equations. Previously, it was stated that the graph of a linear function is indeed a straight line.

A system of linear equations forms when two or more equations are grouped together. The solutions of such a system are the variable values that make all equations within the system true. These solutions are usually found as an ordered pair (x, y), representing the point where the lines intersect on a graph. These intersections provide pivotal insights into the relationship between the equations. For instance, if two lines do not intersect, it means there is no solution, or in other words, there are no variable values that satisfy both equations. On the other hand, if two lines coincide, it means they are the same line, and any point on the line is a solution to both equations.

Graphing is often considered a simpler process than many realize. There are several methods for graphing linear equations, each with its own benefits. For instance, by knowing an equation is linear, you can graph it by finding any two solutions (x1, y1) and (x2, y2). Utilizing tools like online graphing calculators, is advantageous. These calculators can help you visualize the equations and their graphs, helping to learn more about the equations.

The graph of a linear function is not just a visual aid; its a powerful tool for analysis and interpretation. For example, the concept of slope, represented by m in the equation y = mx + b, is central to understanding the behavior of the line. The slope tells us the steepness of the line and the direction of its movement (increasing or decreasing) with changes in x. It describes the rate of change of y with respect to x.

The y-intercept, b, represents the point where the line crosses the y-axis. This is the value of y when x is zero. This is useful in interpreting the context of the linear equation in the real world.

There is a special linear function called the identity function: and its graph: It makes a 45 (its slope is 1) it is called identity because what comes out is identical to what goes in: Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Another way to graph linear functions is by using specific characteristics of the function rather than plotting points.

Let's further illustrate the practical application of linear equations. Consider a scenario where a business is analyzing its costs and revenues. Linear equations can be used to model these elements. For example, fixed costs, such as rent, can be represented as the y-intercept (b), remaining constant regardless of production volume. Variable costs, like materials, can be calculated to determine the slope (m) of the cost line, indicating how costs change with the increase in production (x). The revenue line, similarly, represents the money earned from sales. The point where the cost and revenue lines intersect is the break-even point, a crucial piece of information for any business.

Understanding linear equations opens up a world of possibilities, allowing one to explore, analyze, and predict behavior in diverse fields. From understanding changes in physics to managing finances, from exploring concepts in engineering to even grasping the fundamentals of data analysis, the straight line of a linear equation provides a key to unlock a deeper understanding of the world around us. These equations provide a framework for making informed decisions, from simple scenarios to complex systems. Understanding the equation, how to graph it, and how its parts function are the keys to mastering this essential mathematical concept.

Graphing a linear function, as previously discussed, unveils the visual representation of the equation, offering valuable insights into its characteristics. Whether using a graphing calculator or plotting points by hand, the result is a straight line, a visual testament to the linear relationship defined by the equation.

In conclusion, the study of linear equations is about more than just mathematics. It's about developing problem-solving skills. As you delve into the world of linear equations, embrace the challenges. The rewards are great, empowering you with a fundamental skill that enhances your abilities to understand and impact the world.