Can a single equation truly shape our understanding of the world? The answer, surprisingly, is yes, especially when we delve into the realm of linear functions, those elegant mathematical expressions that underpin so much of what we perceive and interact with daily.

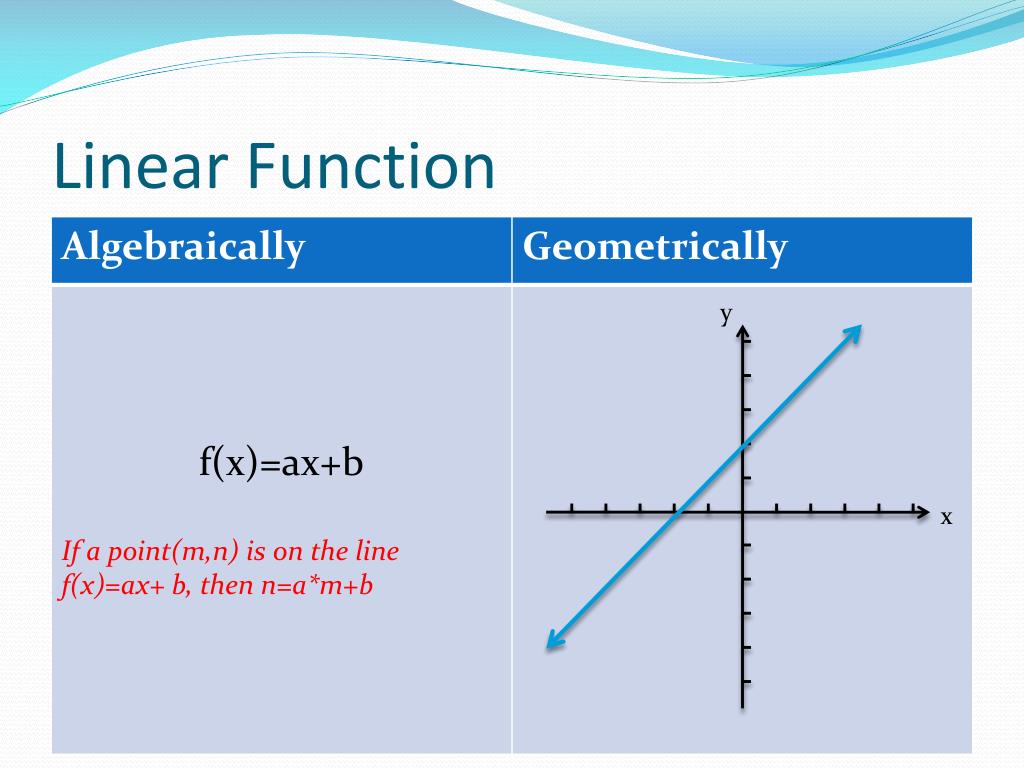
A linear function, at its core, is an algebraic function that, when graphed, manifests as a straight line within a coordinate plane. This seemingly simple definition belies its profound influence. From modeling the trajectory of a projectile to forecasting economic trends, linear functions provide a foundational framework for understanding relationships between variables. They are the building blocks upon which more complex mathematical concepts are constructed, serving as the bedrock for calculus, linear algebra, and beyond. At its simplest, the equation of a linear function is characterized by the variables, 'x' representing the input and 'y' (or f(x)) representing the output and the power of these variables always remain to 1.

Aspect	Details
Definition	An algebraic function that forms a straight line in a coordinate plane. It's a polynomial function with a maximum degree of 1 or 0.
Graph Representation	A straight line, characterized by a constant slope.
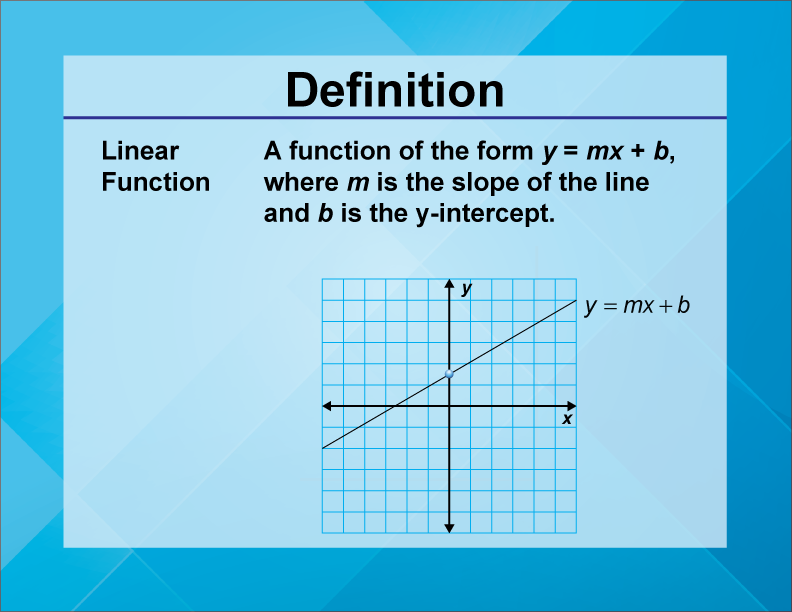
Equation Form	Generally expressed as y = mx + b, where 'x' and 'y' are variables, 'm' is the slope, and 'b' is the y-intercept (initial value).
Slope	Represents the rate of change of the function; calculated as the "rise over run" (change in y over change in x). A positive slope indicates an increase, a negative slope indicates a decrease, and a zero slope represents a horizontal line.
Y-intercept	The point where the line intersects the y-axis; represents the value of 'y' when 'x' is equal to 0.
Degree	The highest power of the variable in the equation. Linear functions have a degree of 1.
Representation Methods	Can be represented in word form, function notation (e.g., f(x) = mx + b), tabular form, and graphical form.
Example	The function describing the train's motion is a linear function.
Examples	f(x) = 2x + 3, y = -0.5x + 1, etc.
Applications	Modeling constant rates of change, calculating distances, representing simple economic models, and more.

For further exploration, consider visiting the following link:
Khan Academy's Linear Equations and Graphs

While linear functions might seem straightforward at first glance, their versatility is what truly sets them apart. They provide an accessible entry point into the world of mathematics, offering a clear illustration of the relationship between variables. The graph of a linear function is a line, has a constant slope, and increases by a constant amount in each time interval, making it possible to visualize the relationship. In contrast to nonlinear functions, which are represented by curves, linear functions maintain a consistent rate of change, a key characteristic that defines their nature.

Think of the simple scenario: if there are 100 fishes in a pond initially, and the population doubles every week, a linear function doesn't capture this growth. Instead, this scenario is better modeled by an exponential function, where f(x) = 100(2)^x, 'x' being the number of weeks. Unlike the consistent growth of a linear function, exponential functions demonstrate a variable rate of change, leading to curves on a graph. The degree of the equation for a nonlinear function will always be greater than 1, marking another key difference.

Linear functions are expressed in a multitude of ways. Consider the train's motion a prime example. The function describing the train's motion is a linear function because it has a constant rate of change. One can represent this function in word form ("The train travels at a constant speed"), function notation, tabular form (a table of distances at specific times), and graphical form (a straight line on a graph). Each representation offers a different perspective on the same relationship, highlighting the adaptability of linear functions.

The relationship between slope and the formula for a linear function is direct. Consider the formula f(x) = ax + b. The term 'a' in this equation represents the slope, while 'b' denotes the y-intercept. Understanding this connection allows one to calculate the slope from the line, or, conversely, create the equation from the slope and y-intercept. A decreasing linear function has a negative slope, as observed in the straight line.

Finding the zeros of linear functions algebraically involves setting y=0 and solving for x. The resulting x-value is the point where the line crosses the x-axis. This algebraic solution should match the one found graphically, providing a verification method.

To represent a linear function, many approaches can be taken. Another approach is using function notation, which provides a concise way to express the relationship between input and output. The equation for a linear function can be written if the slope and initial value are known, giving you control over the shape of the line.

A linear equation is an equation that describes a straight line on a graph. It is an algebraic function that forms a straight line in a coordinate plane and is a polynomial function with a maximum degree of 1 or 0. With these simple elements, we can begin to describe and build models for situations that occur every day.

Conversely, nonlinear functions do not form a straight line, but instead always have a curve. This difference highlights the fundamental distinction between these two types of functions. While linear functions provide a basis for understanding, nonlinear functions can model more complex phenomena with a varying rate of change.

In summary, linear functions are pivotal tools in mathematics. They offer an intuitive framework for understanding relationships and provide a bridge to more advanced mathematical concepts. From plotting simple relationships to serving as a basis for calculus, the influence of linear functions is undeniable.