Are you ready to unlock the secrets hidden within equations and bring abstract concepts to life? Mathematics, often perceived as a realm of cold logic, can be transformed into a vibrant, interactive experience through the power of graphing and visualization.
From the simplest linear equations to complex algebraic expressions, the ability to graph functions, plot data, and visualize equations empowers us to understand mathematical concepts in a more intuitive and engaging way. The ability to animate graphs, adjust sliders, and manipulate parameters dynamically provides a deeper understanding of how changes in equations impact their graphical representations. Whether you're a student, a teacher, or simply a curious mind, mastering the art of graphing is a gateway to a richer and more meaningful appreciation of mathematics. The capacity to visualize, explore, and experiment with mathematical concepts is not just about learning facts; it's about developing the ability to think critically, solve problems, and appreciate the elegance and beauty of mathematical relationships.
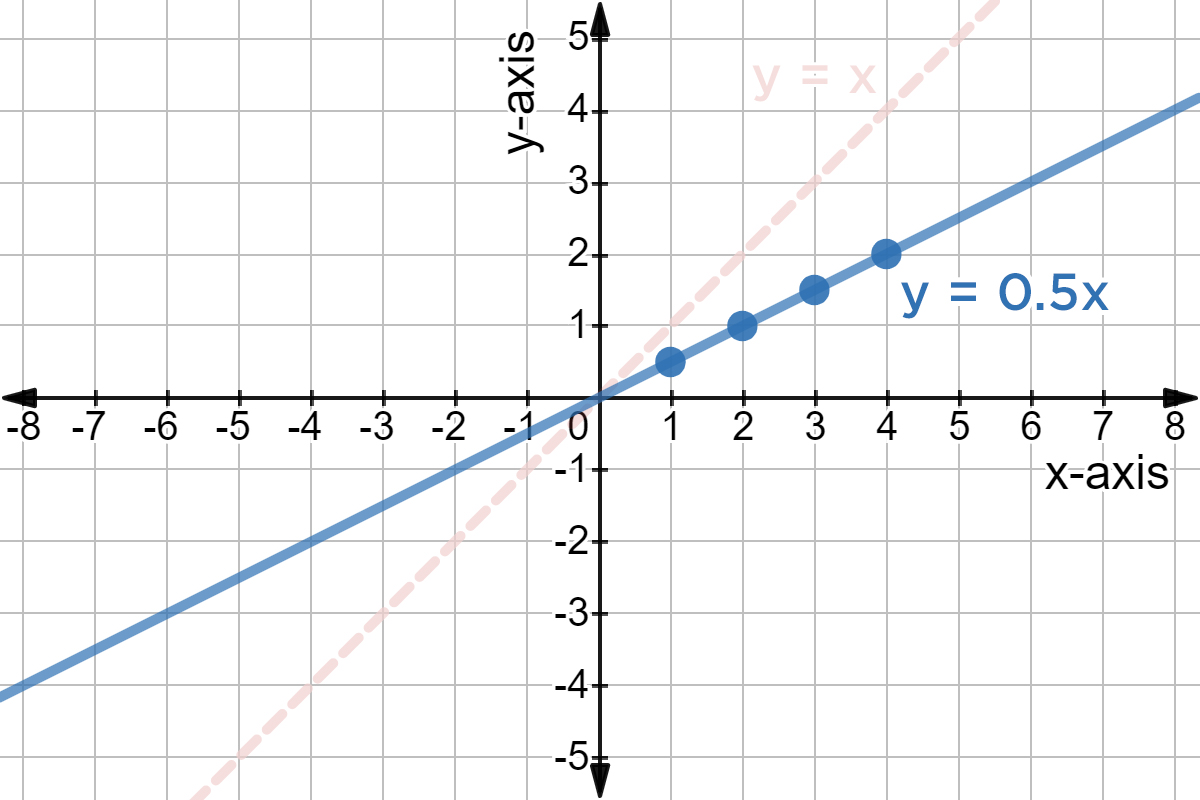
Lets consider the foundation: understanding the core concepts of functions and their graphical representation. A function, at its heart, is a rule that assigns each input value (often represented by 'x') to a unique output value (often represented by 'y' or 'f(x)'). For example, the simple linear equation y = 2x + 3 defines a function. For every value of 'x' we choose, we can calculate a corresponding 'y' value. This pair of (x, y) values represents a point on the graph. By plotting enough of these points and connecting them, we can visually represent the function. In the case of y = 2x + 3, the result is a straight line.
- Bollyflix 4u Movies Download Your Ultimate Guide To Streaming Bollywood Hits
- Celebrity Deep Link How Stars Are Revolutionizing Online Connections
To fully grasp the process, consider the steps involved. First, we determine the function, and the next step is to select values for 'x', then calculate the corresponding values for f(x). This process is known as creating a table of values. For instance, if we choose x = 0, then f(0) = 2(0) + 3 = 3. This gives us the point (0, 3). If we select x = 1, then f(1) = 2(1) + 3 = 5, giving us the point (1, 5). Plotting these points on a coordinate plane and drawing a line through them gives us the graph of the function. This simple process opens doors to understanding other forms and concepts.
Another tool in our arsenal includes exploring the domain of a function. The domain defines all permissible input values for 'x'. In the case of many functions, the domain is all real numbers. However, some functions have restricted domains. For instance, a function that includes a radical like (x) has a domain limited to non-negative values of 'x' because the square root of a negative number is not a real number. Therefore, identifying the domain is the first step in creating a table of values. This step is crucial for graphing, especially in the context of radical functions or functions with denominators.
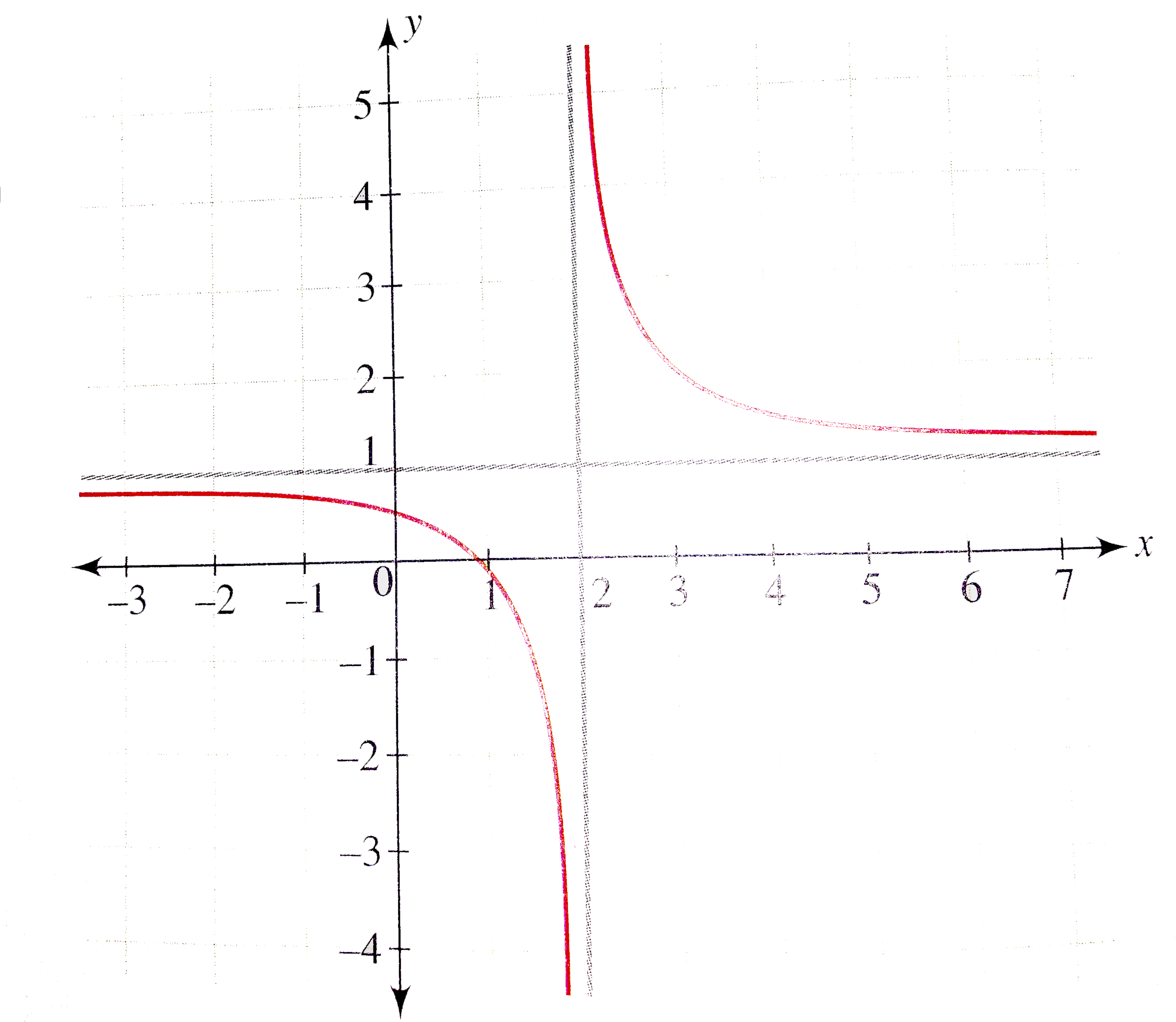
Furthermore, transformations of graphs are essential. The parent function is the most basic form of a specific function type. For example, y = x is the parent function of a parabola. Transformations involve shifting, stretching, shrinking, or reflecting the graph of the parent function. Describing these transformations accurately, step by step, is a vital aspect of mathematical analysis. Consider the function y = 1/x. Compared to the parent function, the graph undergoes transformations involving shifts or vertical stretches. Understanding how these transformations change the appearance of the graph is critical. This understanding extends to rational functions, where identifying asymptotes and undefined points is an important step in comprehending its behavior. You will encounter these concepts if you consider the rational function, particularly by looking at the degree of the numerator and the degree of the denominator, understanding how they influence the overall characteristics of the graph.
- Tonya Westphalen The Inspiring Journey Of A Trailblazer In The Modern Era
- Unlocking The World Of 1tamilblasters Your Ultimate Guide
In the world of mathematics, many resources aid in exploring these concepts. Online graphing calculators from providers such as GeoGebra offer intuitive environments where one can type equations (like y = 2x + 1) and visualize their corresponding graphs. Many calculators offer customization: allow for color selection to differentiate between multiple functions, and providing control of window dimensions (x min, x max, y min, and y max) to view graphs effectively. These tools can also plot data, add sliders to dynamically adjust parameters, and even animate graphs to illustrate the effects of parameter changes.
Beyond individual equations, it's essential to understand standard forms of equations. The general form of a circle's equation is a great example. By recognizing this form, one can identify the circle's center and radius, enabling simple graphing, or to determine important information, like the center and radius of the circle. This highlights how a given equation can be transformed into a visual representation, and how its graphical representation allows for easier interpretation.
To effectively use graphing tools, one must understand the syntax required. For instance, in most graphing calculators, mathematical notation is used. The square of 'x' is written as 'x^2,' the sine of 'x' is 'sin(x),' and the natural logarithm of 'x' is 'log(x).' The capacity to use the right mathematical syntax is essential. Learning to graph is a process, and all elements must be used to build that capability.
Consider a comprehensive example: graphing the function f(x) = 2x + 3. To visualize this, you can choose x values like 0, 1, and 2, calculate corresponding f(x) values (3, 5, and 7, respectively), and then plot the points (0, 3), (1, 5), and (2, 7) on a graph. Since this equation is linear, connecting these points forms a straight line representing the function. This hands-on approach allows for a comprehensive understanding of functions and their visualizations. For more complex equations, tools like graphing calculators can be beneficial to improve visualization.
Moreover, the ability to manipulate and explore graphs becomes more evident through interactive platforms that provide additional functionalities. These platforms provide tools to graph data, allowing you to create a custom graph. Other platforms, like those available on the Stack Exchange network, offer the ability to plot points and visualize algebraic equations. The capacity to add sliders, animate graphs, and perform other interactive tasks makes exploring the world of graphs simple and efficient.
Graphing also enables an examination of the various aspects of parabolas. Discover the properties, and the graphing process can be understood more efficiently with those properties. The ability to graph parabolas involves understanding their key features, like their vertex, axis of symmetry, focus, and directrix. This process allows the creation of various curves and helps solve more complex mathematical problems. By plotting selected points and taking into account the inherent features of the parabola, you can accurately represent the curve and analyze its behavior.
Graphing extends beyond basic functions; it's crucial to grasp more complex functions. Rational functions are a perfect example, where the domain, asymptotes, and behavior at infinity play a critical role. Analyzing the degree of the numerator and denominator can reveal the function's horizontal asymptote and overall shape. This provides deeper insights into the behavior of complex functions.
The principles of graphing and visualization provide a solid foundation for exploring mathematics and beyond. This understanding applies to various disciplines, supporting innovation and discovery.
For further exploration of related subjects and interactive tools, consider the following resources, which allow one to explore and experiment with equations, functions, and their graphical representations:
Interactive, free online graphing calculator from geogebra: Graph functions, plot data, drag sliders, and much more! These sites offer detailed functions, helping students to find a table of values.
| Feature | Description |
|---|---|
| Graphing Functions | Enables the visualization of various equations and functions, including linear, quadratic, exponential, and trigonometric. |
| Plotting Points | Allows plotting individual points on the coordinate plane to visualize data sets or explore relationships. |
| Adding Sliders | Provides interactive controls to adjust parameters in equations, allowing for real-time observation of how changes affect the graph. |
| Animating Graphs | Enables the creation of dynamic visualizations to illustrate the behavior of functions over time or with changing parameters. |
| Customization | Allows users to customize graph appearance by changing colors, axes labels, and gridlines. |
| Equation Input | Accepts standard mathematical syntax for entering equations, making it easy to visualize complex expressions. |
| Data Analysis | Offers tools to analyze plotted data, including finding intercepts, identifying critical points, and measuring areas. |
| Saving and Printing | Enables users to save their graphs as images or print them for documentation and sharing. |
| User Interface | Provides an intuitive and user-friendly interface, making it accessible for both beginners and experienced users. |
| Support | Often includes extensive help sections, tutorials, and community support to assist users. |
The ability to visualize, explore, and experiment with mathematical concepts through the tools outlined here offers a powerful approach to learning and a deep understanding of mathematics. This creates a better way to solve complex problems, understand the world and creates innovative ideas. As you become more familiar with the capabilities of graphing, you'll find the beauty and utility of mathematics.
- Bollyflix 4u Movies Hindi Dubbed Your Ultimate Guide To Bollywood Entertainment
- Ultimate Guide To Ullu Web Series List Your Onestop Destination For Edgy Entertainment