Are you ready to unlock the language of mathematics, where numbers and symbols dance together to reveal the secrets of the universe? Algebraic expressions are the building blocks of this language, empowering us to solve complex problems and understand the world around us in a whole new way.

An algebraic expression, often referred to as a variable expression, is more than just a string of numbers; it's a meticulously crafted mathematical phrase. It's a blend of variables and constants, skillfully interwoven using the fundamental mathematical operators: addition, subtraction, multiplication, division, and exponentiation. These expressions don't stand alone; they are the foundations upon which equations and inequalities are constructed, serving as powerful tools for modeling real-world phenomena and making predictions.

In the realm of algebra, letters take on a special role; they become variables. These are not just symbols; they are placeholders for numbers. They grant us the flexibility to represent unknown quantities, allowing us to generalize and create models applicable to a multitude of situations. The elegance of algebra lies in its ability to transform abstract concepts into concrete solutions.

Algebraic expressions arise when we bring together numbers and variables through mathematical operations. Consider the expression "87," a simple constant. Now, introduce a variable, say "x." Combine them with operations: "x + 5," "2x - 3," or "x^2 + 4x + 7." These combinations, born from variables and numbers, form the very essence of algebraic expressions.

Here's a glimpse into some examples of algebraic expressions:

3x + 5
2y - 7
x^2 + 2x + 1
4ab - 9

These examples only scratch the surface, highlighting the diversity of expressions you might encounter. Remember, the key to mastering algebraic expressions lies in understanding the relationship between the variables, constants, and the operations that bind them. It's about seeing the potential for each expression, not just its current form, and how it can be manipulated to solve equations, inequalities, and model real-world scenarios.

The distributive property is a cornerstone of algebraic manipulation. It allows us to simplify and transform expressions while preserving their mathematical meaning. Consider the expression 2(x + 3). Applying the distributive property, we multiply the 2 by each term inside the parentheses, resulting in 2x + 6. This seemingly simple process opens doors to equation solving and the analysis of more complex expressions.

Imagine two friends, James and Natalie, playing with matchsticks and experimenting with patterns. They might use the matchsticks to create shapes like squares or triangles, carefully arranging them in sequences. If they want to know how many matchsticks they'll need to build the 10th shape in their pattern, they need a formula an algebraic expression that accurately describes the relationship between the shape number and the number of matchsticks.

A variable expression is an expression containing variables alongside numbers, all connected by operations, that defines a mathematical relationship. Examples include 4x + y, 5ab + 33, etc. Mastering these types of expressions is fundamental to unlocking advanced math concepts.

The concept of algebraic expressions is introduced to students in the 7th grade. They will encounter terms related to algebraic equations, such as variables and constants, and start learning to manipulate these expressions.

In algebra, certain letters have specific meanings and are not usually employed as variables. The letters "e" and "i," in particular, have dedicated roles. Similarly, the letter "o" is often avoided because it can be easily mistaken for the number zero (0).

The four basic operationsaddition, subtraction, multiplication, and divisionand their associated signs are crucial to understanding algebraic expressions. Parentheses are used to group terms, representing factors, powers, and exponents. Understanding the role of parentheses is essential in order of operations and simplifies expressions.

Algebra is not just a collection of rules and equations. It's a written skill that requires clarity, efficiency, and precision. It is a systematic method for solving problems, breaking them down into manageable steps, and representing them in a universal language. This means that a solid grasp of variables, constants, and their relationship is essential to solving algebraic problems. A well-structured and carefully written algebraic expression is easier to understand and work with than one that is poorly organized.

Let's put this into practice. Imagine you're at a restaurant, poring over a menu. You want to write an algebraic expression to represent the cost of your meal. The menu is your guide. We can use the first letter of each menu item as a variable. For example, let's say "s" represents the price of a sandwich. If you order two sandwiches, the algebraic expression would be 2s. This introduces the concept of substituting the value of a variable to calculate your total cost. As you'll learn, each expression can become a practical tool for calculating and solving real-life problems.

An algebraic expression is a fundamental concept in algebra, defined as one or more algebraic terms within a phrase. It can consist of variables, constants, and mathematical symbols, such as plus and minus signs. Importantly, it does not include an equals sign (=). For example, "3x^2 + 2y + 7xy + 5" is an algebraic expression.

The ability to understand and manipulate algebraic expressions is pivotal to grasping mathematical principles, rules, and the properties of numbers. Without the knowledge of algebraic symbols and expressions, one cannot fully understand the complexities of mathematics. A single variable, or a combination of mathematical symbols, variables and constants, constitute an algebraic expression.

Consider the following examples to further clarify the concept:

B + 12
N + 8
A + b + 5
0.3 + x
4 m
M - 4
2bc + 8

Each of these examples incorporates variables and constants connected by mathematical operators. This is a crucial point; the ability to dissect these expressions is core to solving for unknown values.

To evaluate an algebraic expression, substitute the given value of the variable. For example, if we need to evaluate "3x + 2" when x = 4, we'd substitute the 4 for x, and the expression becomes 3 * 4 + 2 = 14.

A "term" within an algebraic expression can either be a constant or involve the same variables raised to the same exponents. For instance, "6x^2" and "x^2" are terms within an algebraic expression.

An algebraic expression is a mathematical phrase that uses numbers, variables (letters representing unknown values), and arithmetic operations such as addition, subtraction, multiplication, and division. A key distinguishing feature is that an algebraic expression does not include an equals sign (=). This is what sets them apart from equations.

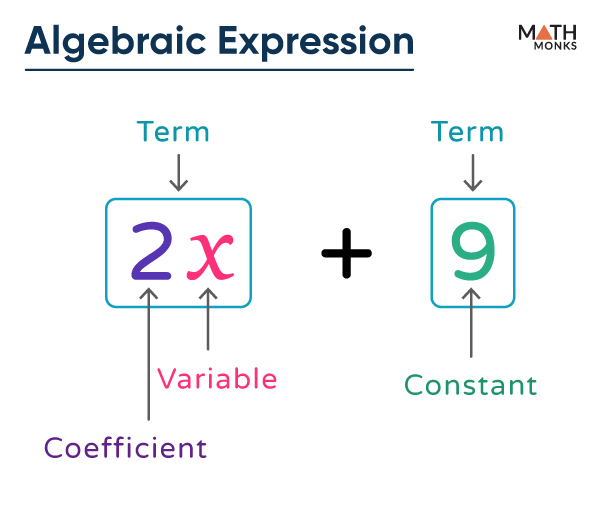
Algebraic expressions are made of terms, which can be a constant or the product of a constant and one or more variables. Examples include 7, y, 5x^2, 9a, and 13xy. The constant that is multiplying the variable(s) is called the coefficient. So in the term "5x^2," the coefficient is "5."

An algebraic expression is a combination of variables, constants, and algebraic operations. It doesn't contain an equal sign. These expressions can be simple or complex, consisting of several terms and operations.

Consider a polynomial comprised of only three terms, known as a trinomial. Examples include x + y + 1, x^2 + 3x + 2, and x^2 + 2xy + y^2. Each of these exemplifies the structure of a trinomial and the use of variables and constants. The terms of a polynomial must share the same variables and the same exponents of those variables.

Variables are the unknown values that are present in an algebraic expression. The unknown values of the expression are represented by these variables, such as "y" and "z" in "4y + 5z". In algebra, these variables become placeholders that can take on a variety of values, depending on the problem or situation. For instance, if we are solving for x, we might find that its value is 3.

When first approaching algebraic expressions, students learn to identify variables, represented by letters, and coefficients, the numbers multiplied by those variables. For example, in the expression 5x + 3, the number "5" is the coefficient, "x" is the variable, and "3" is the constant. The ability to discern these components forms a crucial foundation for manipulating and solving equations.

Mastering algebraic expressions is a journey, not a destination. Practice is crucial. Make sure you apply your knowledge and don't be afraid to make mistakes. The process of working through problems will help you build fluency and a deeper understanding.

The letters e and i have special values in algebra and are usually not used as variables. The letter o is usually not used because it can be mistaken for 0 (zero). These are common conventions.

Variables are used to change verbal expressions into algebraic expressions; these expressions are made of letters that stand for numbers. For instance, "twice a number" can be written as "2x," where "x" represents the unknown number. Verbal expressions and converting these to algebraic expressions is core to mathematics.

Tips for Evaluating Algebraic Expressions:

Replace all occurrences of the variables with open parentheses.
Leave room between the parentheses to substitute the given value of the variable.

These steps will help you in the manipulation of the expressions, it will also enable you to evaluate them correctly, thereby making them a fundamental mathematical skill.