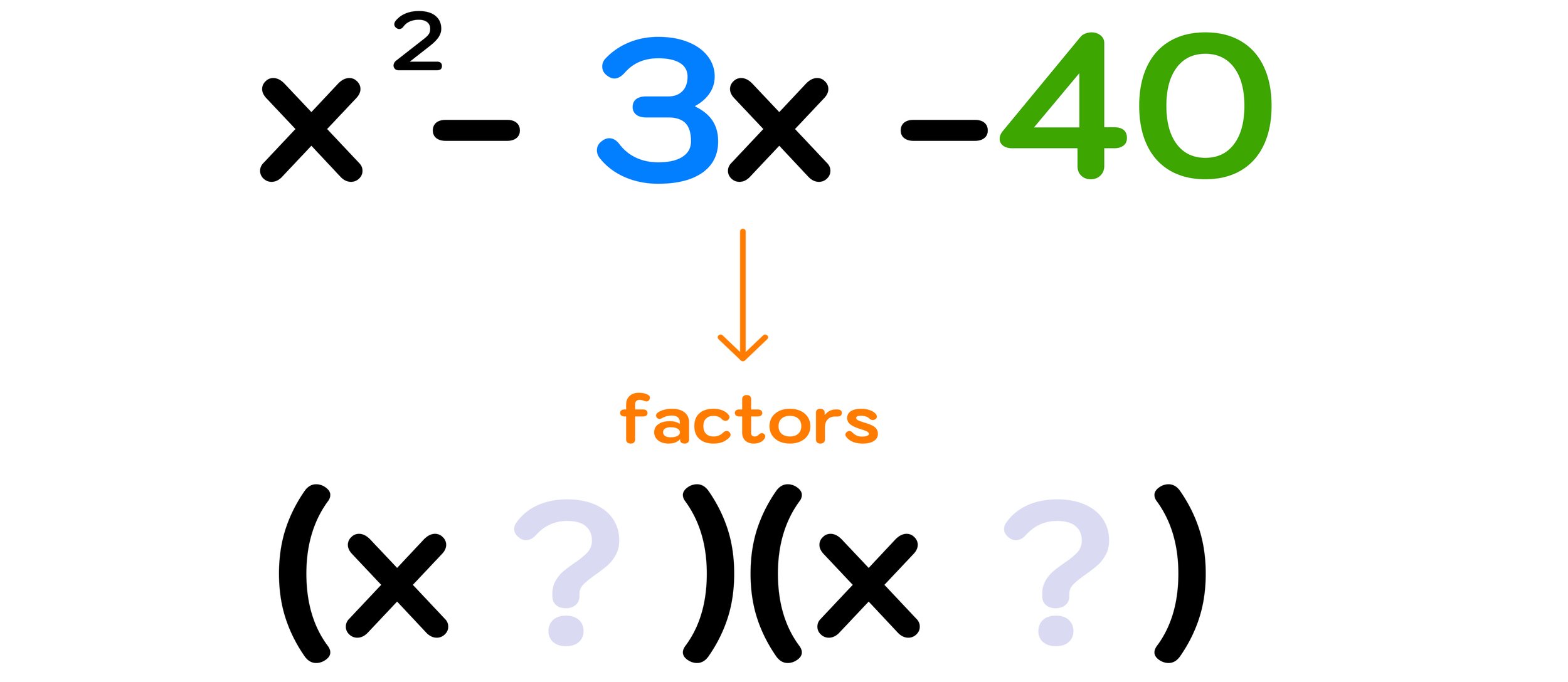Could a seemingly simple mathematical technique hold the keys to unlocking complex problems across diverse fields? Factoring, a fundamental process of breaking down expressions into their constituent parts, is far more than just a textbook exercise; it's a cornerstone of problem-solving that permeates countless aspects of our modern world.
Factoring, at its core, is the act of deconstructing a mathematical expression into its simpler components, known as factors. These factors, when multiplied together, yield the original expression. This seemingly straightforward process has far-reaching implications, making it an indispensable tool in a wide array of disciplines.
This method finds significant utility in algebra, number theory, and even practical disciplines such as engineering, financial modeling, and cryptography. The ability to simplify complex expressions through factorization provides a powerful means to tackle intricate challenges.
- Bolyflixcom Your Ultimate Destination For Streaming Bollywood Movies
- Vegamovies18 Your Ultimate Streaming Destination
One of the core applications of factoring lies in algebra. Solving equations, simplifying rational expressions, and understanding the behavior of polynomials all benefit immensely from the ability to factor. When faced with a quadratic equation, like x + 5x + 4, the goal is to find two numbers that, when added, equal 5 and when multiplied, equal 4. This allows for the equation to be broken down into a more manageable form, leading to straightforward solutions.
| Aspect | Details |
|---|---|
| Key Concept | The process of breaking down a mathematical expression (like a number or a polynomial) into its factors (smaller components). |
| Primary Goal | Simplify complex expressions and equations to facilitate easier solving and analysis. |
| Applications |
|
| Common Techniques |
|
| Tools & Resources |
|
| Importance |
|
| Examples |
|
Consider the practical applications: Engineers use factoring to model and analyze complex systems, while financial modelers employ it to forecast trends and assess risks. Even in the realm of cryptography, the security of many encryption algorithms hinges on the difficulty of factoring large numbers.
The process often begins with identifying the greatest common factor (GCF) of the terms in an expression. This involves finding the largest factor that divides evenly into each term. Once identified, the GCF is placed outside the brackets, and the remaining expression, with each term divided by the GCF, is placed inside the brackets. Verification is done by multiplying the factors to ensure they yield the original expression.
- Yupmoviecom Netflix Your Ultimate Streaming Haven
- Filmyflyworld Your Ultimate Destination For Entertainment And Beyond
For those tackling quadratic equations, the process can involve finding two numbers that add up to a specific value (the coefficient of the x term) and multiply to another (the constant term). This method allows for the quadratic to be rewritten into a factored form, revealing its roots.
The world of factoring also extends to number theory, where prime factorization plays a central role. Breaking down a number into its prime factors is essential in various algorithms and cryptographic applications.
Various visual tools are available to aid in understanding factoring. Algebra tiles, both physical and digital, help students to connect the visual representation of area models with the abstract concept of factoring. Such tools provide a tangible way to grasp the relationships between factors and expressions.
Collaborative learning is another vital aspect of mastering factoring. Working in groups allows students to share different perspectives, problem-solving strategies, and learn from each other's insights. Worksheets, while offering practice, benefit when combined with these collaborative exercises.
These worksheets are specifically designed to focus on the practical application of factoring and solve problems using factoring. They also offer a comprehensive resource to help students grasp key concepts, such as greatest common factors, factoring by grouping, and factoring trinomials.
Factoring is not a standalone skill; its woven into the fabric of other mathematical concepts. Its importance becomes evident as one progresses to advanced mathematical domains, where it serves as a fundamental tool for solving problems.
Factoring is not just about academic proficiency; its a skill you will find yourself employing in many daily situations. The ability to simplify and break down complex problems into their core components is valuable in everyday decision-making.
For those seeking additional practice and guidance, a wealth of resources is available. Practice problems and worksheets, such as those available on Khan Academy, offer solutions for a wide range of factoring problems. You can also explore "Algebra factoring lessons" with examples and practice problems to deepen understanding.
When dealing with quadratic functions (polynomial functions of degree two), factoring becomes particularly important. Understanding the roots of a quadratic equation is essential to understand the behavior of the function, and these factorizations are helpful when faced with problems. Combined with formulas such as Vieta's formulas, these are excellent techniques.
The techniques of factoring polynomials are adapted based on the number of terms. A monomial is already in factored form, and the first type of polynomial to consider for factoring is a binomial. Factoring by grouping and the difference of squares are critical methods to learn.
Mastering factoring involves understanding different strategies. It involves understanding techniques such as finding the greatest common factor, factoring by grouping, and recognizing special forms such as the difference of squares. Additionally, learning how to factor trinomials (polynomials with three terms) by various methods is crucial.
A typical example is using the Pythagorean theorem: One leg of a right triangle is 3 feet longer than the other leg, and the hypotenuse is 15 feet. The problem will be approached by factoring the quadratic equation and solving for the dimensions of the triangle.
For those interested in delving deeper, online resources provide complete answer keys and detailed explanations, which can significantly aid the learning process. These resources allow students to learn how to factor polynomials of different degrees and forms with examples and explanations.
So, embrace the practice of factoring. It's a skill that transcends the boundaries of textbooks and classrooms, equipping you with the analytical tools to dissect and solve problems across various fields.
Whether you're solving equations, simplifying expressions, or tackling real-world problems, factoring remains an indispensable skill. As you explore the world of mathematics, you'll discover that this seemingly simple technique has a profound impact on our understanding of numbers, equations, and problem-solving.
- Bollyflix 4u Movies Hindi Dubbed Your Ultimate Guide To Bollywood Entertainment
- Lara Rose Birch Leak The Untold Story You Need To Know