Is there a hidden elegance in the world around us, a subtle order that dictates form and function? Symmetry, the mirror image of ourselves, reveals a profound truth about the universe, a truth that can be found in the curve of a leaf, the structure of a snowflake, or the mathematics of a parabola.
We often perceive symmetry intuitively, a sense of balance that pleases the eye. However, to truly understand and utilize symmetry, we need to delve into the underlying principles. The core question lies in whether an equation remains unchanged when we employ symmetric values. The answer to this question unlocks doors to various forms of symmetry, each with its unique characteristics. The study of symmetry is not limited to visual observations; it is a rigorous investigation that demands an understanding of mathematical principles and their real-world applications.
Here is the table with the information about Axis of symmetry in mathematical terms.
- Penelope Menchaca Onlyfans The Ultimate Guide To Her Rise Content And Success
- Bollyflix Vip Com Your Ultimate Destination For Bollywood Entertainment
| Aspect | Details |
|---|---|
| Definition | The axis of symmetry is a line that divides a shape or a function into two identical halves that are mirror images of each other. |
| Type of Symmetry | It can be found in various shapes, including parabolas, ellipses, and hyperbolas (shapes often created when solving quadratic equations). |
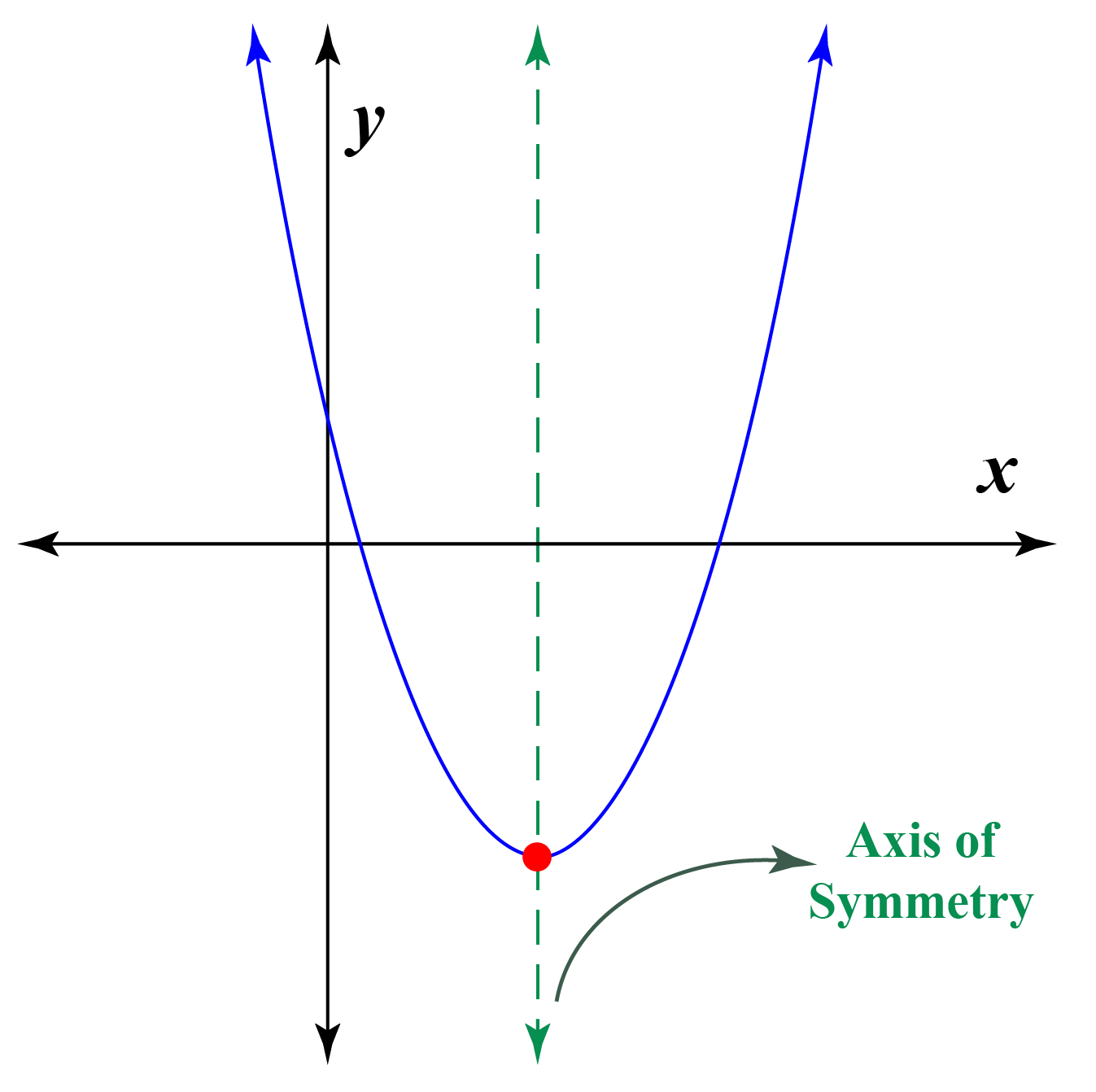
| Parabola | In a parabola, the axis of symmetry is a vertical line passing through the vertex, the highest or lowest point on the curve. |
| Ellipse | An ellipse has two axes of symmetry, the major and minor axes, which intersect at the center of the ellipse. |
| Hyperbola | A hyperbola also has two axes of symmetry, intersecting at the center, that are related to the vertices and foci of the hyperbola. |
| Formula for Parabola's Axis | For a parabola defined by the equation y = ax + bx + c, the axis of symmetry is given by the formula x = -b / (2a). |
| Calculation Steps | To find the axis of symmetry:
|
| Importance | Understanding the axis of symmetry is crucial for graphing quadratic functions, analyzing the properties of shapes, and solving related mathematical problems. |
| Applications |
|
| Tools | Online tools and calculators are available to find the axis of symmetry for specific functions or shapes. |
| Examples |
|
| Lines of Symmetry in Basic Shapes |
|
| Vertex | The axis of symmetry always passes through the vertex of a parabola. |
| Vertex Formula | The x-coordinate of the vertex can be found using the axis of symmetry formula. The y-coordinate can be calculated by substituting the x-coordinate into the original quadratic equation. |
| Reflection Symmetry | The axis of symmetry is also known as the line of reflection. |
| Visualization | Graphing tools can help visualize the axis of symmetry on a parabola by plotting the equation of the parabola. |
| Advanced Concepts | Exploring the axis of symmetry helps in understanding the properties of parabolas, their focus, and directrix, especially for students taking math lessons in schools or in their online courses. |
| Online Resources | You can easily find axis of symmetry calculators online that often give step-by-step solutions. |
Reference: Maths is Fun
To embark on this journey of understanding, we can start with a simple premise: Is the equation unaltered when we use symmetric values? This query serves as a guiding light, and the process of checking for symmetry hinges on the type of symmetry at hand. Symmetry manifests in various ways, from the reflectional symmetry seen in a parabola to the rotational symmetry found in a circle. The approach we take to verify symmetry is tailored to the specific form we're investigating.
Online tools, such as axis of symmetry calculators, have become invaluable resources. These calculators, often equipped with formulas, guide users through the process of evaluating vertex forms and identifying the axis of symmetry, whether it's for a parabola, an ellipse, or a hyperbola. They typically provide step-by-step results, making complex mathematical concepts accessible and easier to understand. Graphing calculators, which are available online, offer the ability to plot functions, visualize algebraic equations, and even animate graphs. These tools not only aid in understanding the concept of symmetry but also provide an interactive environment for exploration. One can plot points, join them with smooth curves, and observe the symmetry in action.
- Sky Movie Hd Your Ultimate Guide To Streaming Highdefinition Movies
- Ullu New Web Series 2024 The Hottest Buzz In Digital Entertainment
The axis of symmetry, a crucial element in understanding parabolas, divides the curve into two perfectly congruent halves. The axis itself generally passes through the vertex of the parabola, serving as the line of reflection. To calculate this axis, one needs to understand the equation of the parabola, typically expressed in standard form. The derivation of the axis of symmetry begins with the quadratic function y = ax + bx + c. By applying the appropriate formula, we can pinpoint the location of this important line.
Symmetry goes beyond mathematical constructs; it is deeply embedded in our world. Bilateral symmetry, for example, is evident in the human face and certain architectural designs. This type of symmetry is best visualized through frontal projections, where one side mirrors the other. In essence, the right image is a reflection of the left image, created by flipping the original picture horizontally by 180 degrees. It is evident in the arrangement of elements or points that create mirror images.
Various shapes have different numbers of lines of symmetry. A square boasts four lines of symmetry, a rectangle has two, and a circle has an infinite number of them. A parallelogram, however, lacks any line of symmetry. Regular polygons with 'n' sides possess 'n' axes of symmetry. The axis of symmetry is best understood in the context of a parabola, specifically when graphing a quadratic function. By finding the axis of symmetry, one can understand the properties of the curve, like its vertex, focus, and directrix.
The symmetrical axis is often referred to as the line of symmetry, producing a mirror image that reflects on each side of the parabola. The formula used to determine the axis of symmetry for a parabola equation is crucial. For a parabola, the equation is typically in the form of y = ax + bx + c, and the formula to calculate the axis of symmetry is x = -b / (2a). This equation helps determine the vertical line that splits the parabola into two equal parts.
When working with a parabola's equation, identifying 'a', 'b', and 'c' is essential. Once these values are known, plugging them into the formula x = -b / (2a) provides the x-coordinate of the axis of symmetry. This process provides a clear roadmap for calculating the axis of symmetry, which is vital in understanding the traits of a parabolic curve. The axis of symmetry is a vertical line that bisects a parabola into two mirror-image halves. It serves as the line of reflection that passes through the vertex of the parabola.
For a parabola in standard form, the equation is a cornerstone. The axis of symmetry is a vertical line cutting the parabola into two identical halves. When faced with a quadratic function in the form f(x) = ax + bx + c, calculating the axis of symmetry becomes straightforward. You can find the axis of symmetry by using the formula, which highlights how to calculate it. For example, if you have an equation and identify 'a', 'b', and 'c', you can find the axis of symmetry. This is a valuable exercise for the vertex and axis of symmetry using a graphing calculator.
In essence, the axis of symmetry (AOS) is a vertical line that splits a parabolic curve into two equal parts. It's a crucial concept for graphing quadratic equations. When trying to find the axis of symmetry, one aims to find the line passing through the vertex and the focus. This line is the axis of symmetry, a fundamental concept in quadratic equations. As you advance in your studies, you will find that mastering this concept is a gateway to a deeper understanding of the shapes around us.
- Bollyflix Official Site Your Ultimate Destination For Bollyflix Movies
- Leah Halton Naked A Candid Look At The Controversy And Beyond