Can a single number truly hold the key to unlocking complex mathematical mysteries? The concept of a "constant," an unchanging value, is far more pivotal than many realize, forming the bedrock upon which equations and expressions are built.
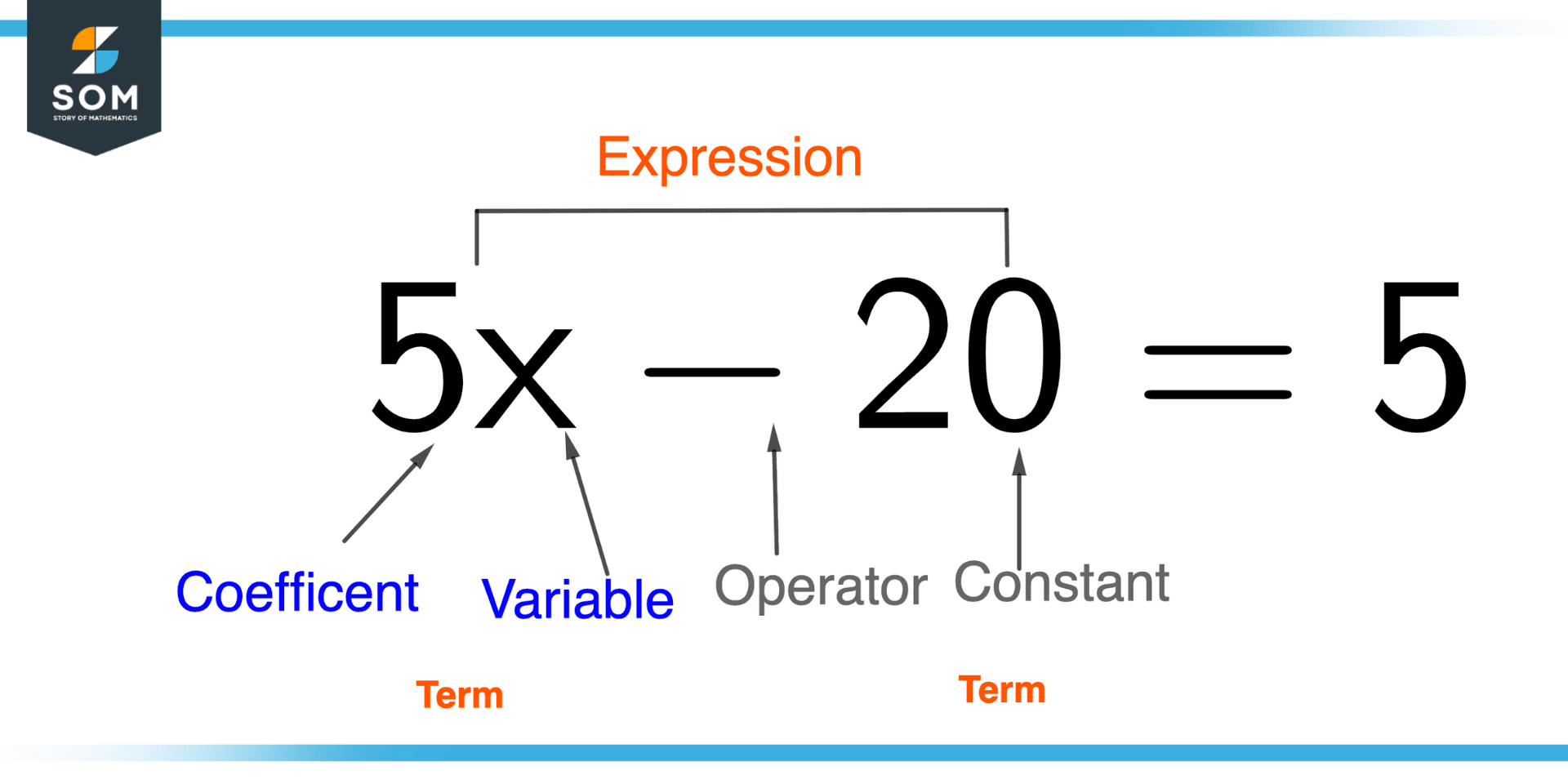
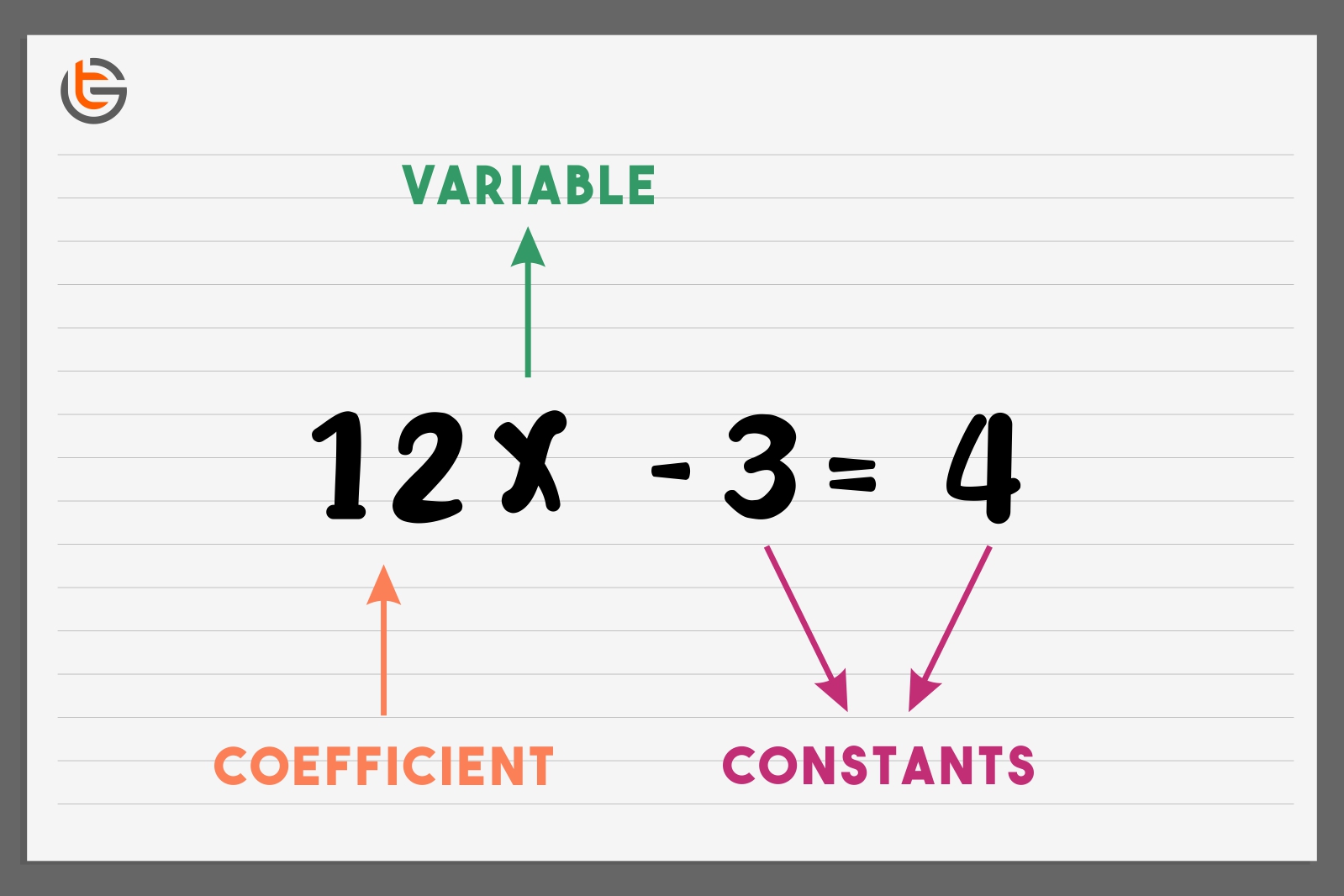
In the realm of mathematics, a constant reigns supreme as a steadfast value, a numerical anchor that remains impervious to the fluctuations of variables. This steadfastness distinguishes constants from their dynamic counterparts, the variables, which dance and shift within the framework of equations. Consider the equation "x + 5 = 9." Here, the numbers 5 and 9 are the constants, the fixed points around which the variable 'x' finds its solution. In the more general form "y = ax + b," 'a' and 'b' stand firm as constants, while 'x' and 'y' are the variables that are free to vary according to values of each other. These are the very essence of algebra.
Understanding constants goes beyond simple recognition; it involves grasping their diverse roles and implications in various mathematical contexts. Mathematical constants, as distinguished from physical constants, are often denoted by symbols or named after mathematicians, facilitating their use across multiple mathematical problems. These constants are the unchanging foundations upon which mathematical structures are erected.
- Bollyflix 4u Movies Download Your Ultimate Guide To Streaming Bollywood Hits
- Khatrimaza 4k Movies Download Your Ultimate Guide To Highquality Entertainment
The true essence of a constant lies in its immutability. Whether it's a solitary number or a symbolic representation, the constant remains unwavering. This stability underpins mathematical operations, offering a reliable framework for calculations. It serves as a reference, a point of stability, when equations need to be solved. Its used while graphing functions, and during different mathematical functions as well.
In equations and expressions, constants stand in contrast to variables, which change. They can be seen as the building blocks or the parameters against which variables operate. They contribute to the unchanging nature of math and the ability to solve different equations.
Consider a simple algebraic expression like "3x + 5." The constant here is '5,' a standalone number not multiplied by a variable. Similarly, the mathematical symbol '' (pi) is a well-known constant term representing the ratio of a circle's circumference to its diameter, a value approximately equal to 3.14159. This is another example of the role of constants in mathematics.
- The Bollyflix Movies Your Ultimate Guide To Streaming Bollywood Magic
- Bollyflix Movie Your Ultimate Destination For Bollywood Entertainment
Constants can also take the form of coefficients or parameters. A coefficient is a number, often a single digit, that multiplies a variable. In the expression "4x," the coefficient is 4. Coefficients and constants together shape the behavior of equations and expressions. In contrast, parameters represent fixed values that may influence the characteristics of a function or equation but do not themselves change during the analysis. Parameters are also constants, but they have an added dimension. They can be changed in the function in the same way we change coefficients.
To pinpoint a constant within an algebraic expression, one should seek terms devoid of variables. These standalone numbers or symbols that denote a known value are the constants. For instance, in the quadratic polynomial x + 2x + 3 = 0, the term '3' is a constant. The constant term, also referred to as the free term, provides a basis to find the correct answer.
Functions, whether they involve algebraic expressions or not, rely on the concept of constants. The output of a constant function will always remain constant regardless of the input. It's a demonstration of a constant term, where the output is always the same.
The utilization of constants extends to the field of geometry as well. In every triangle, the constant characteristic of three sides defines the shape. This fixed feature supports the principles of shapes and figures.
Throughout mathematical calculations, constants are vital, offering a sense of stability and serving as reference points for solving equations, graphing functions, and executing diverse mathematical operations.
The power of constants lies in their unwavering nature. They are unchangeable quantities, usually represented algebraically, forming the backbone of mathematical expressions and equations. They provide stability, ensuring that mathematical operations remain consistent and predictable.
In more advanced mathematical discussions, the term "constant" is often reserved for real, non-integral numbers of interest, while "number" is used when discussing interesting integers. In certain contexts, such as linear combinations, constants have many applications.
A constant term can be a coefficient, a parameter, or a mathematical constant. The characteristics of a constant are that it is an unchanging number.
The application of these concepts is pivotal in simplifying and solving algebraic equations. Constants, as the fixed points in this mathematical environment, assist in the process of solving equations, graphing functions, and performing various other mathematical tasks.
The ability to recognize constants and distinguish them from variables is a core mathematical skill. Identifying constants within an equation or expression is the first step toward understanding how the different parts interact to create a mathematical relationship.
In the realm of algebra, terms, coefficients, and constants play a critical role in defining expressions and equations. These terms are necessary to master the concepts of mathematics.
The term "constant of proportionality" is also important. It refers to a constant value, typically denoted by the variable 'k,' which connects two variables in either a direct or inverse variation. This k is often used in multiple equations.
The study of constants opens doors to understanding complex mathematical concepts. From simple arithmetic to advanced calculus, constants provide the stability and structure that makes mathematical operations possible.
Here is a table that will help you to understand the concepts of constants in mathematics:
| Concept | Description | Examples |
|---|---|---|
| Constant | A value that does not change within a given mathematical context. It's a fixed number or a symbol representing a fixed number. | 5 in the equation x + 5 = 9, (pi) 3.14159, the number 3 in x + 2x + 3 = 0 |
| Constant Term | A term in an algebraic expression or equation that does not contain any variables. It's a standalone number. | The '3' in the expression x + 2x + 3, the '5' in the equation y = 3x + 5. |
| Coefficient | A number or symbol that multiplies a variable in a term. | The '3' in the term 3x, the 'a' in the expression ax + b. |
| Mathematical Constant | A key number whose value is fixed by an unambiguous definition. | (pi), e (Euler's number) |
| Constant Function | A function that always outputs the same value, regardless of the input. | f(x) = 7 (for any value of x, the output is always 7). |
Constants are an integral part of algebra, assisting in providing a stable platform for solving equations, and supporting various algebraic operations. These fixed values enable the consistent application of mathematical principles.
To broaden the understanding of the topic, here's a brief exploration of additional mathematical concepts:
| Concept | Description | Examples |
|---|---|---|
| Variable | A symbol (usually a letter) that represents an unknown or changeable value. | x, y, z |
| Algebraic Expression | A combination of variables, constants, coefficients, and mathematical operators. | 3x + 5, y = ax + b |
| Equation | A mathematical statement that asserts the equality of two expressions. | x + 5 = 9, y = 3x + 5 |
| Function | A relationship between a set of inputs and a set of permissible outputs, where each input is related to exactly one output. | f(x) = 2x + 1, f(x) = c (constant function) |
By grasping the significance of constants, one gains a deeper understanding of mathematical principles. This skill is especially helpful for students, enabling them to navigate the complexities of algebra with greater confidence.
- Xgroovy The Ultimate Platform For Digital Content Creators
- Unlocking The World Of 1tamilblasters Your Ultimate Guide