Ever wondered how mathematicians solve complex problems, build models, and unravel the mysteries of the universe? The answer, in large part, lies in the seemingly simple concept of a variable.

At its core, a variable is a symbol, often a letter, that represents a number or quantity that can change or take on different values. This fundamental idea is the cornerstone of algebra and is woven throughout the fabric of mathematics, physics, computer science, and countless other disciplines. But what exactly are these variables, and why are they so crucial?

Variables aren't just confined to algebra, however. They can also represent functions, allowing mathematicians to explore relationships between different quantities. In more advanced fields, variables take on even more diverse roles, standing in for sets, vectors, and other abstract mathematical objects. The beauty of a variable is its versatility. It's a placeholder, a container, a symbol of the unknown, all rolled into one.

Lets consider a basic algebraic equation: X + 2 = 4. Here, 'X' is our variable. It represents a value that, when added to 2, equals 4. In this case, the value of X is easily determined to be 2. This simple example underscores the fundamental purpose of variables: to allow us to formulate equations and solve for unknown quantities.

Mathematics often employs letters from the alphabet to represent variables. 'X' is perhaps the most commonly used, not because it holds any inherent mathematical significance, but simply because it is easily recognizable and doesn't favor any particular number. Variables like 'y' and 'z' are also frequently employed, especially when dealing with multiple unknowns or relationships. The choice of letter is largely arbitrary; the key is that it serves as a symbol to represent an unspecified value.

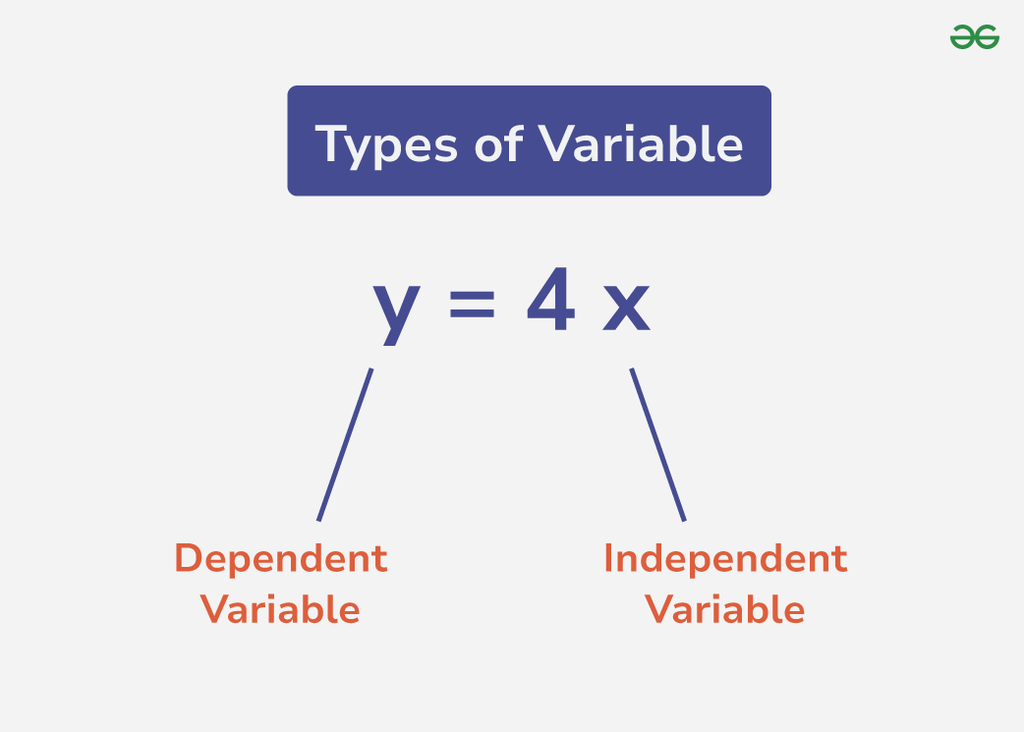
Delving deeper, we encounter two critical types of variables: independent and dependent variables. An independent variable is one whose value can be changed or controlled, while a dependent variable is affected by the independent variable's value. For example, in a function like y = x + 2, 'x' is the independent variable, and 'y' is the dependent variable. As we change the value of 'x', the value of 'y' changes accordingly.

Understanding the difference between independent and dependent variables is crucial in various fields, including statistics and experimental studies. In scientific research, for example, scientists manipulate independent variables to observe their effects on dependent variables, helping to establish cause-and-effect relationships.

Variables, in essence, act as placeholders in mathematical expressions and equations. They allow mathematicians to generalize relationships and solve problems without having to know specific numerical values at the outset. They represent unknown quantities, making it possible to manipulate and analyze equations to find solutions. Consider the equation, 2x + 3 = 7. Here, 'x' is the variable, representing the unknown number we are trying to find. By manipulating the equation using algebraic principles, we can solve for 'x' and determine its value.

The concept of a variable has evolved over time, but it remains a cornerstone of mathematical understanding. From the ancient Egyptians, who used symbols to represent unknown quantities, to modern calculus, where variables play a central role, this concept has been essential to advancements in mathematics. Variables enable us to formulate general rules, model real-world phenomena, and solve complex problems across a wide array of disciplines.

But how are variables actually used in the context of solving mathematical problems? The following sections delve into the practical application of variables, exploring how they are employed in various branches of mathematics, from arithmetic to calculus. These sections provide examples and illustrations to demonstrate the versatility and power of variables in different contexts.

The true power of variables becomes evident when we consider their use in expressions and equations. In an expression, a variable represents an unknown value that can be substituted with a number to obtain a result. For instance, in the expression '2x + 5', we can substitute any number for 'x' to find the corresponding value of the expression. Equations, on the other hand, express relationships between variables and numbers, allowing us to solve for unknowns and analyze mathematical relationships. The ability to manipulate variables is essential for simplifying equations and isolating the unknown.

The use of variables is not confined to any particular branch of mathematics; they are a common thread that runs through arithmetic, algebra, geometry, trigonometry, calculus, and many other areas. In arithmetic, variables are used to represent unknown numbers in simple equations. In algebra, they play a central role in solving for unknowns, formulating equations, and representing relationships between quantities. In geometry, variables are used to represent lengths, angles, and other geometric elements.

Consider the equation y = 5x + 9, for example. The value of the variable 'y' will vary with the estimation of the value of variable 'x.' Thus, we can say that 'y' is a dependent variable, and 'x' is an independent variable. It is important to recognize the significance of these variables to understand the functions, equations, and formulas.

The ability to distinguish between independent and dependent variables is crucial for understanding mathematical relationships. The independent variable is the input value that the experimenter can alter, and the dependent variable is the output value whose value is determined by the input value. Understanding the variables allows for a comprehensive understanding of experiments and equations.

In conclusion, variables represent unknown or changing quantities, making them essential for generalizing relationships and solving complex problems across many fields. Understanding the different types of variables and how they interact is fundamental to mathematical concepts.

Let's take an in-depth look at how variables function within the intricate framework of mathematical principles, and how they work to help us solve problems.

The following table summarizes the key aspects of what defines and differentiates variables.

Aspect	Description	Examples
Definition	A symbol (usually a letter) representing a number, quantity, or value that can change or is unknown.	x, y, z, a, b, c
Purpose	To represent unknown quantities, allow for generalization, and facilitate the solving of equations and the modeling of relationships.	Finding the value of 'x' in the equation 2x + 3 = 7; Modeling the relationship between distance and time.
Types	Independent variables (input values), dependent variables (output values), discrete, continuous, categorical.	In the equation y = 5x + 9, x is independent, y is dependent.
Usage	Used in equations, expressions, formulas, and functions across all branches of mathematics.	y = mx + b (linear equation), A = r (area of a circle)
Key Characteristics	Placeholders for unknown values; can take on multiple values; essential for algebraic manipulation.	In the expression x + 5, x can equal any number.