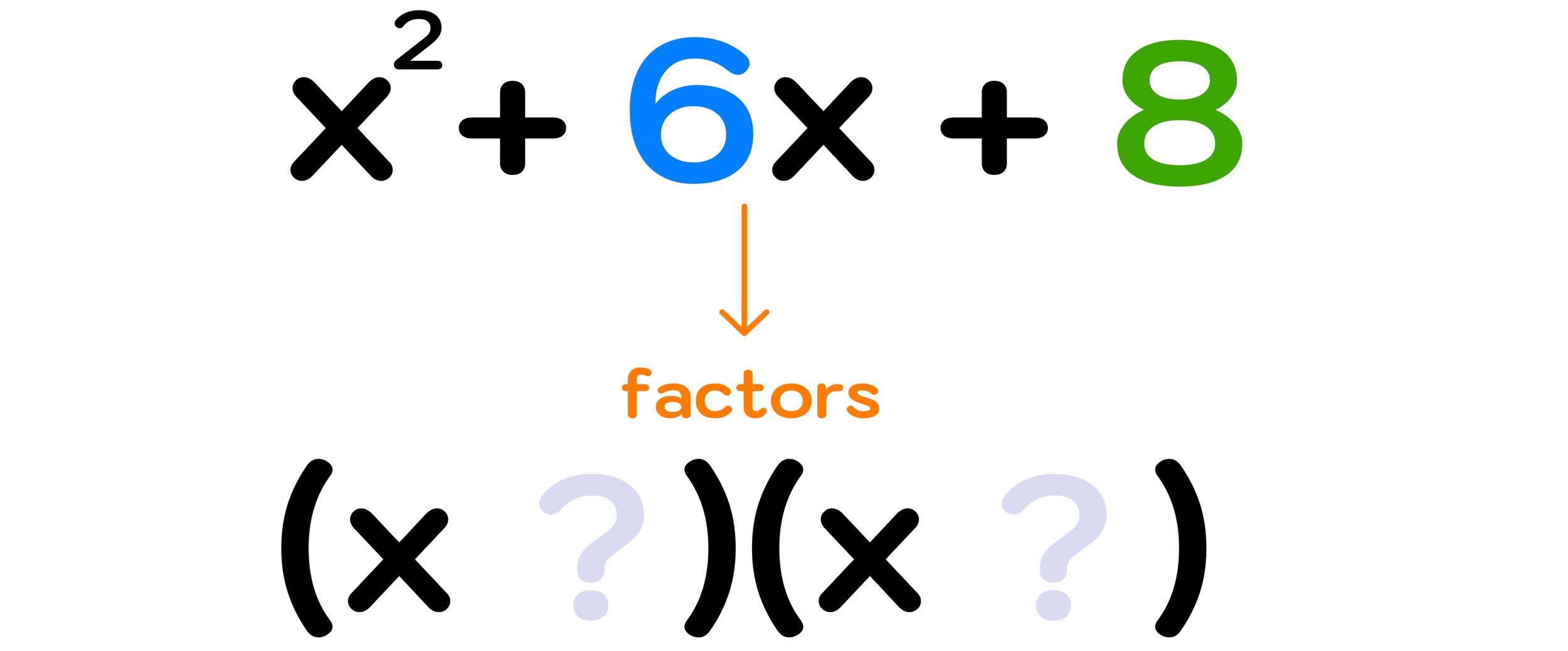Why is factoring in mathematics considered a cornerstone of algebraic manipulation? Because it unlocks the ability to simplify complex expressions, solve equations with ease, and reveal the underlying structure of mathematical relationships.
Factoring, often referred to as factorisation (especially in the UK), is a fundamental process in mathematics. It's the art of breaking down an expression into its constituent parts, the factors. Think of it like dismantling a complex machine to understand how each gear, lever, and spring contributes to its overall function. In algebra, this "machine" is a mathematical expression, and factoring is the method to reveal its building blocks.
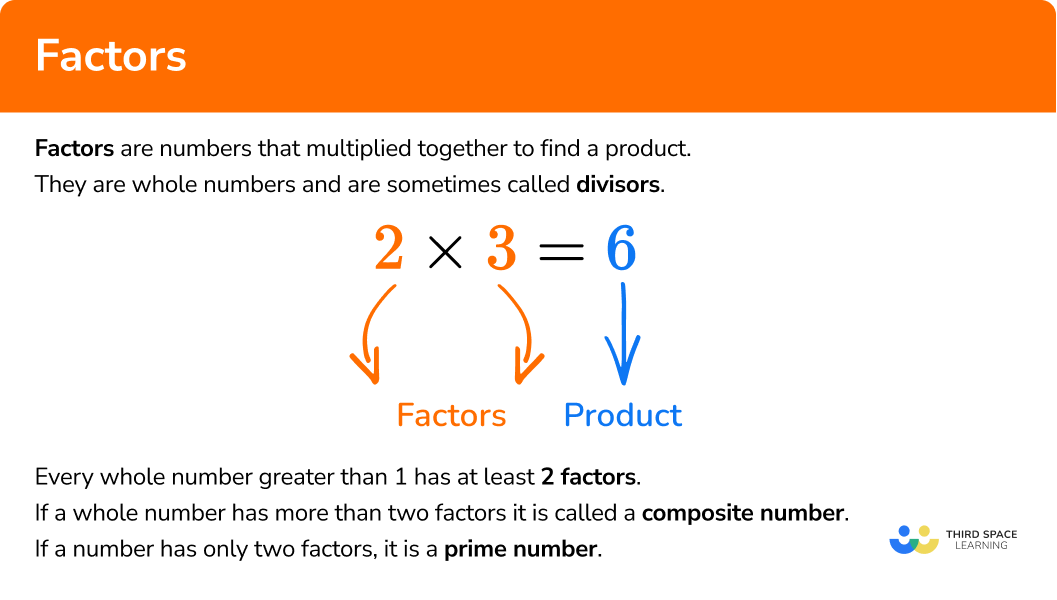
At its core, factoring involves finding what multiplies together to form a given expression. It is like splitting an expression into a multiplication of simpler expressions. This process allows mathematicians to rewrite mathematical expressions as products of their factors. This skill is essential for simplifying equations, solving for unknown variables, and understanding the underlying relationships within a mathematical problem.
- Filmyflyworld Your Ultimate Destination For Entertainment And Beyond
- Desicamnet The Ultimate Hub For Photography Enthusiasts
Factoring essentially reverses the multiplication process. By breaking down complex expressions into simpler, more manageable parts, factoring provides a powerful tool for problem-solving. It's the inverse of the distributive property, the rule that allows us to expand expressions by multiplying a term across a sum or difference. The result? A more direct route to the solution.
There are various strategies to approach factoring. These methods are like different keys that unlock the same door. One common technique is to factor out the greatest common factor (GCF) of each group of terms and then factor out the common binomial factor. Sometimes, when factoring by grouping, it is necessary to rearrange terms to find that common binomial factor. The key is that after factoring out the GCF, the remaining binomial factors must be identical for this technique to work. Another popular method involves recognizing patterns, like the difference of squares or perfect square trinomials.
At the heart of it all, factoring is the process of expressing a given integer or polynomial as a product of its prime factors or irreducible components. Prime numbers, indivisible by any number other than 1 and themselves, serve as the foundation of factoring. The unique and irreducible nature of prime factorization is a cornerstone of number theory, guaranteeing that the breakdown of a number into its prime factors is unique. For example, consider the number 24. Its prime factorization is 2 2 2 3. This unique combination is the only way to represent 24 as a product of prime numbers.
- Wwwfilmyfly Your Ultimate Destination For Entertainment And Beyond
- Bollyflix Official Site Your Ultimate Guide To Bolly Flix
It is important to remember that we can factor other mathematical objects, such as polynomials. Polynomials are algebraic expressions consisting of variables and coefficients. Factoring polynomials allows us to simplify them, solve equations, and uncover critical information about their behavior. Factors, then, are the building blocks of an expression, just like how numbers can be broken down into prime factors. They reveal the fundamental components that make up a more complex structure.
The purpose of factoring expressions is to get a simplified version. This version is easier to work with while finding values of an unknown variable. For example, the number 16 can be factored as 1 x 16, 2 x 8, and 4 x 4. Therefore, 1, 2, 4, 8, and 16 are the factors of 16.
This exploration of factors and factoring in algebra provides a glimpse into the world of simplifying and manipulating mathematical expressions. Factoring itself is a method of expression simplification that involves identifying patterns between the terms of the expression.
In mathematics, factorisation or factoring is defined as the breaking or decomposition of an entity (for example, a number, a matrix, or a polynomial) into a product of another entity, or factors. These factors, when multiplied together, give the original number, matrix, or expression. This concept is frequently taught in lower secondary classes, often starting around grades 6 to 8, depending on the curriculum.
Factoring is a fundamental mathematical technique where smaller components, the factors, help simplify numbers or algebraic expressions. This approach is widely used in algebra, number theory, and practical fields like engineering, financial modeling, and even cryptography, where it forms the basis of many security algorithms.
Factoring algebra involves factoring algebraic terms. It's like splitting an expression into a multiplication of simpler expressions. For example, the expression 2y + 6 can be factored as 2(y + 3). This simplification is particularly useful when dealing with variables and solving equations.
Factoring can be seen as the opposite of expanding, which involves multiplying out terms. The most common methods used for prime factorization are the factor tree and division methods. For example, consider finding the prime factors of 100 using these methods. The prime factors of 100 are 2 and 5, and its prime factorization is 2 2 5 5.
Algebraic expressions can be formed as products of factors. To factor in algebra, the usual first step is identifying the greatest common factor (GCF) of the terms within an expression. For example, if faced with an expression like 3x + 6x, a 3x can be pulled out to obtain 3x(x + 2).
Factoring simplifies expressions, it is an essential skill in algebra. This simplification is key to solving equations by revealing their roots, the values of the variable that make the equation true. For example, the polynomial x + cx + d, where a + b = c and ab = d, can be factorized into (x + a)(x + b). This reveals the roots of the quadratic equation.
In mathematics, factorization (or factorisation) consists of writing a number or another mathematical object as a product of several factors, typically smaller or simpler objects of the same kind. This is the process of breaking down a complex entity into its fundamental building blocks. This is a journey of mathematical exploration. A student already knows, which then moves on to creatively crafting a fresh concept in young minds. Done in a way that is relatable and easy to grasp, which will stay with them forever.
A factor, in mathematics, is a number or algebraic expression that divides another number or expression evenlythat is, with no remainder. For example, 3 and 6 are factors of 12 because 12 3 = 4 exactly and 12 6 = 2 exactly. Other factors of 12 include 1, 2, 4, and 12. A factor is the value that divides a number or expression equally without any leftovers.
Prime factorization is the method that allows every integer greater than 1 to be expressed as the product of prime integers. It's the foundation for understanding the structure of numbers.
What is a factor in math? A factor is a number that divides another number evenly. The factors of a number all go into that number evenly, so they are the perfect components.
Factoring is a typical mathematical procedure for separating the components (or numbers) that multiply to generate a new number. There are several components in certain integers. For example, when you multiply the factors of 6 and 4, 8 and 3, 12 and 2, and 24 and 1, you get the number 24. This illustrates that different combinations of factors can result in the same product.
Many online tools are available to help with factoring. By entering an expression into a factoring calculator, complex expressions transform into a product of simpler factors. These calculators can factor expressions with polynomials involving any number of variables and also more complex functions. This is a useful tool for checking your work and understanding the process.
When learning to factor, start with polynomials with 2 terms, known as binomials. The first step when factoring a polynomial is to look for a GCF, a greatest common factor, that all the terms have in common. Identifying and factoring out the GCF is often the first step towards simplifying the expression.
The factor of a number, in math, is a divisor of the given number that divides it completely, without leaving any remainder. This perfectly dividing method highlights the fundamental relationship between factors and their parent numbers. In order to find the factors of a number, we can use different methods like the division method and the multiplication method. The division method systematically checks for divisibility, while the multiplication method looks for pairs of numbers that multiply to the given number.
Let's consider some examples of factors in math. For instance, 5 is a factor of 10, 15, 20, and 25. This is because 10 5 = 2, 15 3 = 3, 20 5 = 4, 25 5 = 5, and so on. Any number in the 5 times table has 5 as a factor.
When finding factors, it's useful to look for them in pairs, as two factors will multiply to make another number. It's a systematic approach that simplifies the process of factorization.
A math factor is a number you multiply with others to get to your desired number. A number is a factor if it divides evenly into the desired number. The resulting answer is also a factor. This is a clear and concise definition that captures the essence of what a factor is.
Factoring is the process of decomposing or splitting any given polynomial into a product of two or more polynomials. It is the reverse of multiplication, breaking down a larger expression into its building blocks.
A factor tutor is an expert in math who helps students understand the idea of factors. These tutors are like guides, offering clarity, encouragement, and providing a solid understanding of the math of factors. Factors are an important part of math, but there isn't a specific kind of math tutor who only works with them. It's usually taught in elementary school. Depending on the school and district, it can be introduced as early as the 4th grade.
In conclusion, factoring (factorising or factorizing) is the process of splitting an algebraic expression and writing it as a product of its factors. Factors are building blocks of an expression, like how numbers can be broken down into prime factors. It is a skill that forms the foundation for many higher-level math concepts, making it a crucial tool for anyone studying mathematics.
| Concept | Description | Importance | Methods | Applications |
|---|---|---|---|---|
| Definition | The process of breaking down a mathematical expression (number, polynomial, etc.) into a product of its factors. | Simplifies expressions, solves equations, reveals the underlying structure of mathematical relationships. |
|
|
| Factors | Numbers or expressions that, when multiplied together, result in the original expression. | Building blocks of mathematical expressions, revealing fundamental components. | Understanding the components of a problem. | |
| Prime Factorization | Decomposition of a number into a product of its prime factors. | Foundation for number theory; ensures unique representation. |
|
|
| Greatest Common Factor (GCF) | The largest factor that divides two or more numbers or expressions evenly. | Essential for simplifying expressions and factoring. | Simplifying algebraic fractions. | |
| Applications | Real-world uses of factoring. | Highlights the usefulness of factoring in different disciplines. |
|
Reference website:Maths is Fun
- 18 Vegamovies Your Ultimate Guide To Plantbased Cinematic Adventures
- Emily Tamara Pois The Rising Star Redefining The Entertainment Scene