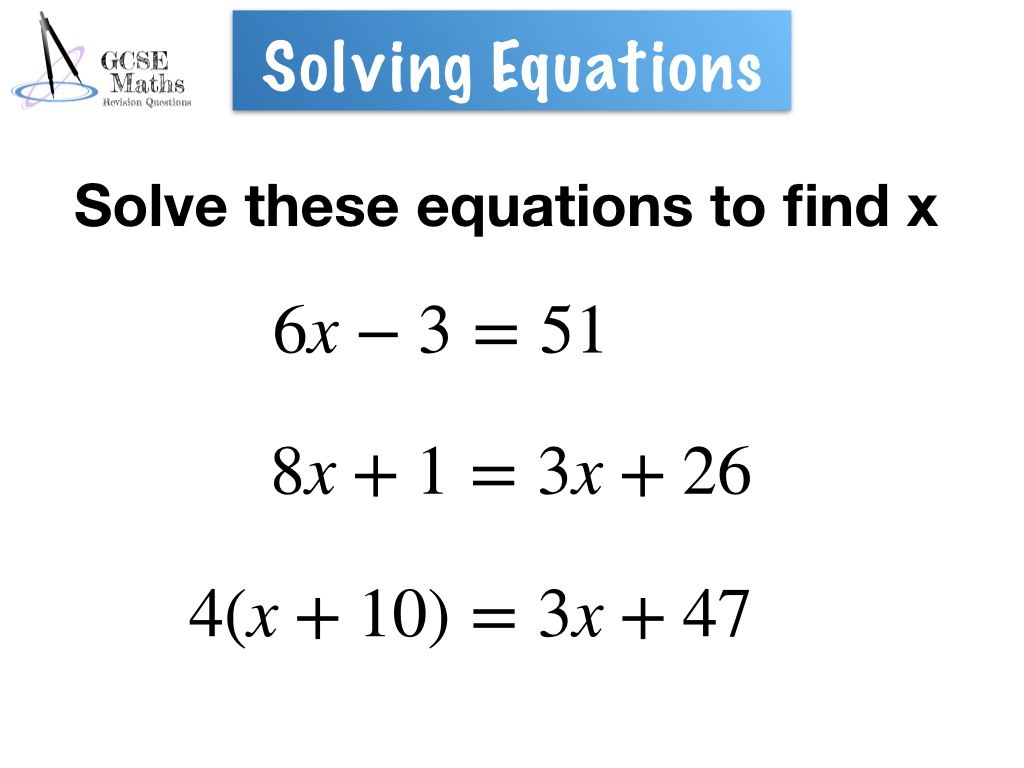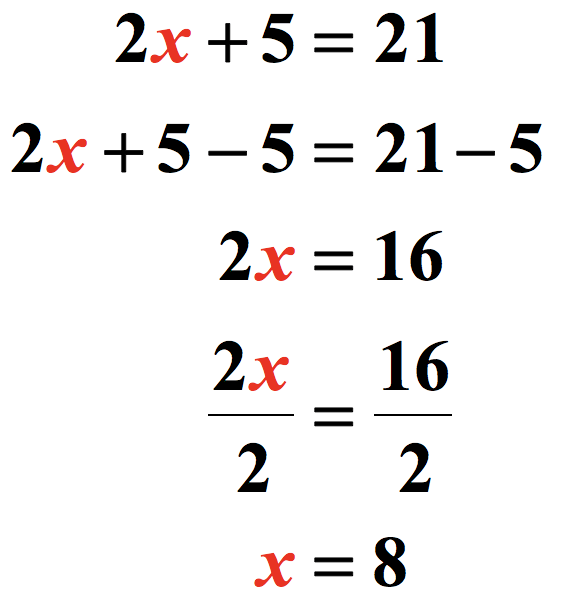Can manual calculations truly keep pace with the demands of modern mathematics? The limitations of manually solving linear equations highlight the increasing need for efficient, automated solutions in a world driven by complex calculations.

Manually solving linear equations, a foundational skill in mathematics, presents several challenges that can hinder progress and efficiency. While the ability to solve these equations by hand remains a valuable asset, it's essential to acknowledge the drawbacks associated with this approach, particularly in today's fast-paced environment. These limitations often necessitate the use of alternative methods, such as equation solvers and calculators, to optimize the problem-solving process.

The process of solving equations is fundamentally about determining the value(s) of a variable that satisfy the given condition, making the equation true. Whether it's a basic linear equation or a more intricate quadratic, rational, or radical equation, the goal remains the same: to isolate the variable and identify its value. However, the method of achieving this varies significantly depending on the type of equation and the chosen approach. While manual solving offers a clear understanding of the underlying principles, it often struggles when faced with complexity and time constraints.

Aspect	Details
Core Function	The objective is to find the value(s) of a variable that make the equation true.
Equation Types	Encompasses linear, quadratic, rational, and radical equations, each presenting unique challenges.
Methods	Manual solving, which can be time-consuming; and automated methods like equation solvers.
Complexity	The complexity of the equation directly impacts the time and effort required to solve it.
Efficiency	Automated solutions become increasingly attractive as complexity and the need for rapid results increase.
Understanding	Manual solving provides a deeper understanding of the underlying mathematical principles, useful for learning.
Applications	Foundational skill in many STEM fields, used in calculations, modelling and data analysis.

Solving equations by hand is a valuable skill, but it can often be a slow process. This is particularly true when dealing with systems of equations, or when fractions or decimals are involved. The time spent on these calculations can quickly escalate, hindering productivity, and potentially leading to errors. This delay can be especially problematic in fields where rapid calculations are critical, and in scenarios demanding intricate systems of equations.

The equations themselves come in many forms. The spectrum of equations extends from simple linear equations to quadratic equations, rational equations, and even radical equations, each demanding specific techniques for their resolution. Understanding these distinctions and mastering the techniques required for each type is crucial for effective problem-solving. Quadratic equations, for instance, present a slightly greater level of complexity than their linear counterparts, often requiring the application of specific formulas or methods.

Mastering the fundamentals is crucial; those uncertain about linear equations should review the foundational concepts before tackling more advanced topics. Interactive tutorials and solvers can be invaluable tools for learning about quadratic formulas and other advanced techniques. Platforms like Wolfram|Alpha offer robust equation-solving capabilities, leveraging the Wolfram Language's "solve" and "reduce" functions. These encompass a broad range of methods suitable for various algebraic problems, from fundamental linear and quadratic equations to complex multivariate nonlinear systems. The power of such tools lies not just in their speed but also in their capacity to handle diverse mathematical problems.

The user-friendly interface is a key attribute. The ability to simply type an algebra problem into a text box and receive immediate results simplifies the learning process significantly. This approach eliminates the need for manual calculations and permits a focus on comprehension. Furthermore, this feature serves as a learning instrument for the user, by showing each step of solving the equation, enhancing the grasp of the approach.

Solving an equation is essentially identifying the value of the unknown variable within the equation that results in the equation's condition being true. Variables, the unknown elements in an equation, can be on either side of the equals sign. They are the unknowns we aim to isolate and determine. The process aims at finding the unknown part, a fundamental task in algebra, and the core purpose behind solving equations.

Equation solvers often allow users to specify whether they require approximate numerical answers or exact solutions, and how many digits of accuracy are necessary. This flexibility is critical, as it allows the equation to be solved to a level of precision appropriate to the specific problem. This level of control is often unavailable when solving manually.

Math equations are fundamentally statements built upon algebraic expressions linked by an equals sign. They employ defined mathematical formulas that can be addressed through techniques like substitution. These formulas are the frameworks that link two or more variables, helping us determine unknown variables through the substitution of known values. They are the building blocks for mathematical problem-solving.

Equation calculators provide the user with a step-by-step solution to an algebraic equation. They guide users through the processes required to simplify and solve equations, and with explanations for each step, they aid in the learning process. To solve for a variable like 'x,' the equation has to be manipulated to isolate 'x,' allowing the user to discover the value of the variable.

These digital tools, such as the one offered by quickmath, facilitate the manipulation of mathematical expressions. They expand, factor, or simplify various expressions, cancel common factors, split fractions, and consolidate multiple fractions into one. This feature set significantly reduces the workload and potential for errors, particularly when handling more complex calculations.

Equation solving tools usually provide the exact answers, while numerical answers can be used when necessary. This flexibility gives the user a great advantage when solving complex equations. Furthermore, online math solvers provide free step-by-step solutions to problems in algebra, calculus, and other mathematical areas. This supports a variety of educational demands, and the flexibility of use makes it a valuable learning tool.

Equation calculators are also a powerful mathematical instrument that swiftly and effectively solves equations. They streamline intricate calculations and ensure that users understand both the method and the solution. These tools also support the student's capacity to recognize and correct mistakes, which helps them master the material.

Algebraic equations with exponents require a unique approach. The process involves isolating the exponent on one side of the equation and subsequently removing the exponent by finding the root of both the exponent and the constant on the other side. This technique is specific to exponential equations, ensuring the correct resolution.

The equation calculator can handle many types of equations to determine the best solution. Once the equation is entered, the system produces the results, presenting the solution in the most efficient method. The user gets a reliable resolution in a short period.

In many cases, multiple operations are required to solve equations, making the use of the order of operations (PEMDAS) crucial. This ensures each step is in the correct order. Students studying mathematics, algebra, geometry, and physics also encounter word problems. These problems involve interpreting data, generating equations, and calculating the appropriate response.

Substitution is another useful method. When using substitution to solve a system of equations, one equation is solved for a variable, and this expression is substituted into the other equation. Solving the resulting equation for the remaining variable and substituting this value back into the original equation yields the value of the other variable. This methodical approach enables a step-by-step procedure.

Consider an example of an algebraic equation such as x + 3 = 2x. Solving this equation involves isolating x on one side. If an equation has fractions, multiplying every term by the denominator will help in solving it. Similarly, if the distributive property is involved (parentheses), the equation should be rewritten accordingly. By following these methods, users are able to find the solution to the equation accurately.

Method	Description
Manual Solving	Solving equations by hand, useful for building understanding but can be slow and prone to error with complex equations.
Equation Solvers	Online calculators or software that automatically solve equations, providing step-by-step solutions and supporting various equation types.
Substitution	Solving one equation for a variable and substituting that expression into the other equation to solve systems of equations.
Order of Operations (PEMDAS)	A set of rules determining the sequence of operations in calculations to avoid errors and ensure accurate solutions.
Exponents	Isolating the exponent and removing it by finding the root of both sides of the equation for efficient solving.