Is there a hidden elegance within the curves and forms we encounter daily, a secret code that governs perfect balance? The answer lies within the axis of symmetry, a fundamental concept that unlocks the secrets of shapes, equations, and the very structure of our world.
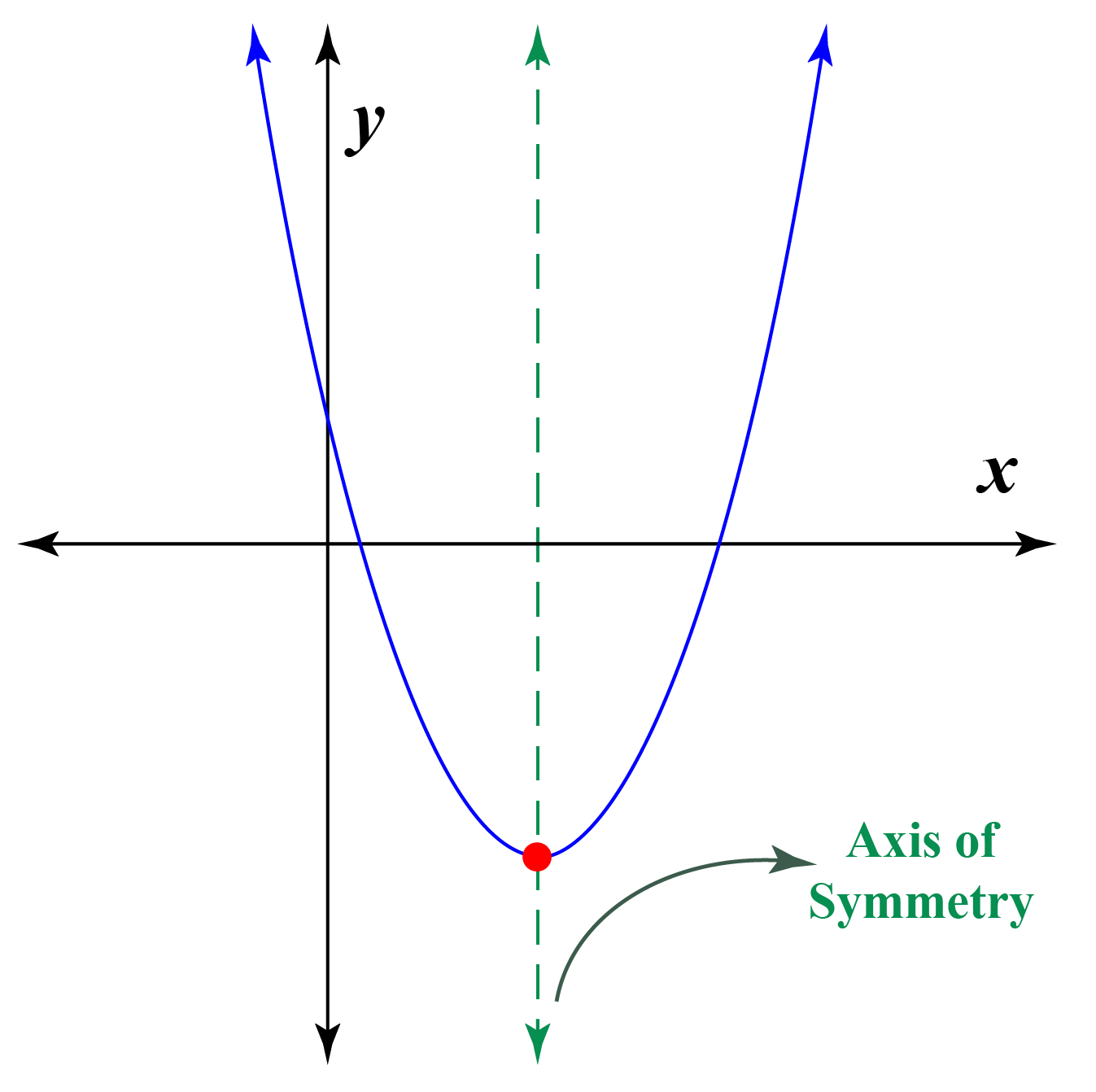
The concept of symmetry is more than just an aesthetic principle; it is a fundamental building block of mathematics and the natural world. From the intricate patterns of snowflakes to the graceful arcs of a bridge, symmetry provides both aesthetic appeal and structural integrity. In the realm of mathematics, the axis of symmetry acts as a critical tool, allowing us to understand and manipulate complex shapes and equations. Consider the familiar parabola, the U-shaped curve that represents quadratic equations. The axis of symmetry is the vertical line that perfectly bisects this curve, providing a crucial point of reference for analyzing its behavior. Understanding the axis of symmetry is key to sketching parabolas, identifying their roots, and solving related equations.
Let's delve deeper into the world of symmetry.
| Concept | Details | Relevance |
|---|---|---|
| Axis of Symmetry | A line that divides a shape into two congruent (identical) halves, creating a mirror image. It can be an imaginary line. | Fundamental to understanding shape properties, aids in calculations, and provides a reference point for analyzing mathematical functions. |
| Parabola | The U-shaped curve representing quadratic equations. | Axis of symmetry helps find roots (solutions) and graph parabolas. |
| Reflectional Symmetry | A shape has reflectional symmetry if one half is the mirror image of the other. The axis of symmetry acts as the line of reflection. | Allows us to classify and understand shapes. |
| Vertex | The highest or lowest point on a parabola. This point always lies on the axis of symmetry. | Essential in determining the maximum or minimum value of the quadratic function. |
| Standard Form of a Quadratic Equation | The form: ax2 + bx + c | Formula to find axis of symmetry: x = - b/2 a is directly applicable. |
| Vertex Form of a Quadratic Equation | The form: a(x - h)2 + k | Axis of symmetry easily identifiable: x = h. |
| Congruent Parts | Identical in shape and size. | Crucial in understanding the symmetry properties. |
For the sake of example, let's say we are going to find an axis of symmetry of a parabola. The axis of symmetry is the vertical line that goes through the vertex, dividing the parabola into two equal parts. The parabola equation can be expressed in two ways: standard form and vertex form. The axis of symmetry formula is the formula to calculate the axis of symmetry.
Imagine folding a piece of paper. The crease created by the fold acts as an axis of symmetry, dividing the paper into two identical halves. This same principle applies to geometric shapes. A square has four axes of symmetry, while an equilateral triangle has three. More complex forms can also have symmetry, such as those found in art or natural forms.
The axis of symmetry is not the same as the vertex; rather, the axis of symmetry always passes through the vertex of the parabola.
- Bolyflix Net Your Ultimate Streaming Destination Unveiled
- Bollyflix In The Ultimate Destination For Bollywood Enthusiasts
In the world of parabolas, the axis of symmetry becomes an incredibly useful tool. It offers a point of reference which lets us work with the functions.
To locate an axis of symmetry, one might check the degree or largest exponential value of the polynomial. If the degree of a polynomial is 2, you can use the axis of symmetry formula. This formula can be used to find the axis of symmetry for any parabola.
Let us examine some practical applications and formulas to locate and use the axis of symmetry effectively:
The axis of symmetry corresponds to the symmetric line for the graph of a quadratic function, which is a parabola. Having a reference for the symmetry gives a lot of information about the parabola. For example, the roots of the equation will be disposed symmetrically with respect to this axis of symmetry.
One of the basic steps is to locate the degree or the largest exponent in a polynomial.
For the purpose of illustration, let's say that we want to find the axis of symmetry of a parabola given by the equation. You can use the following equation to find the axis of symmetry: x = - b/2 a. For example, If the equation is in the form ax2 + bx + c, the axis of symmetry will be the vertical line x = - b/(2 a).
Therefore, for every equation in the standard form, one can find the axis of symmetry and the vertex.
If a parabola is in vertex form, the axis of symmetry is easily identified. In the vertex form a(x - h)2 + k, the axis of symmetry is the vertical line x = h. The vertex of the parabola is at the point ( h, k).
Let's consider an example: If a parabola has the vertex form f(x) = 2(x - 3)2 + 1, the axis of symmetry is x = 3, and the vertex is (3, 1).
This means that a vertical line can be drawn at x = 3 which perfectly cuts the parabola in half.
The axis of symmetry is the key in understanding how reflectional symmetry works. If the shape is folded in half over the axis, both parts will appear as mirror images.
A shape has reflectional symmetry if it looks the same after being reflected. The line of reflection is called the axis of symmetry, and it splits the shape into two congruent equal similar halves. Some figures can also have more than one axis of symmetry.
Another way to think about it is that if the shape were to be folded in half over the axis, the two halves would be identical as mirror images.
The axis of symmetry is an important concept in geometry, and the formula for finding the axis of symmetry of a line or curve is relatively simple. In general, the axis of symmetry is the line that divides a figure into two halves that are mirror images of each other.
The axis of symmetry divides the parabola into two identical halves. For a parabola, the axis of symmetry always passes through the vertex. By knowing the axis of symmetry, you automatically know the x-coordinate of the vertex.
Now, let us find the axis of symmetry of the a function. Also consider the example of how to find axis of symmetry on a graph.
In the given image, the vertical line through the vertex is the axis of symmetry. For a parabola the axis of symmetry always passes through the vertex.
Consider the equation of parabola. The axis of symmetry of this parabola will be the line x = \u2212 b 2 a.
The axis of symmetry is also known as line of symmetry. Any shape that can be folded down a line to get two matching halves is said to have a line symmetry.
The axis of symmetry is a vertical line; The axis of symmetry is the vertical line that goes through the vertex, dividing the parabola into two equal parts.
In essence, the axis of symmetry is a tool for revealing and simplifying the structure of shapes.
The axis of symmetry is an imaginary line that splits a shape or object into two or more identical parts.
- Unveiling Mydesilatest Your Ultimate Guide To Trending Desi Content
- Filmyflysite Your Ultimate Destination For Movie Entertainment