Are you ready to unlock the secrets hidden within the visual language of mathematics? The world of graphs is a powerful tool, capable of transforming abstract equations into tangible representations that reveal hidden patterns and relationships.

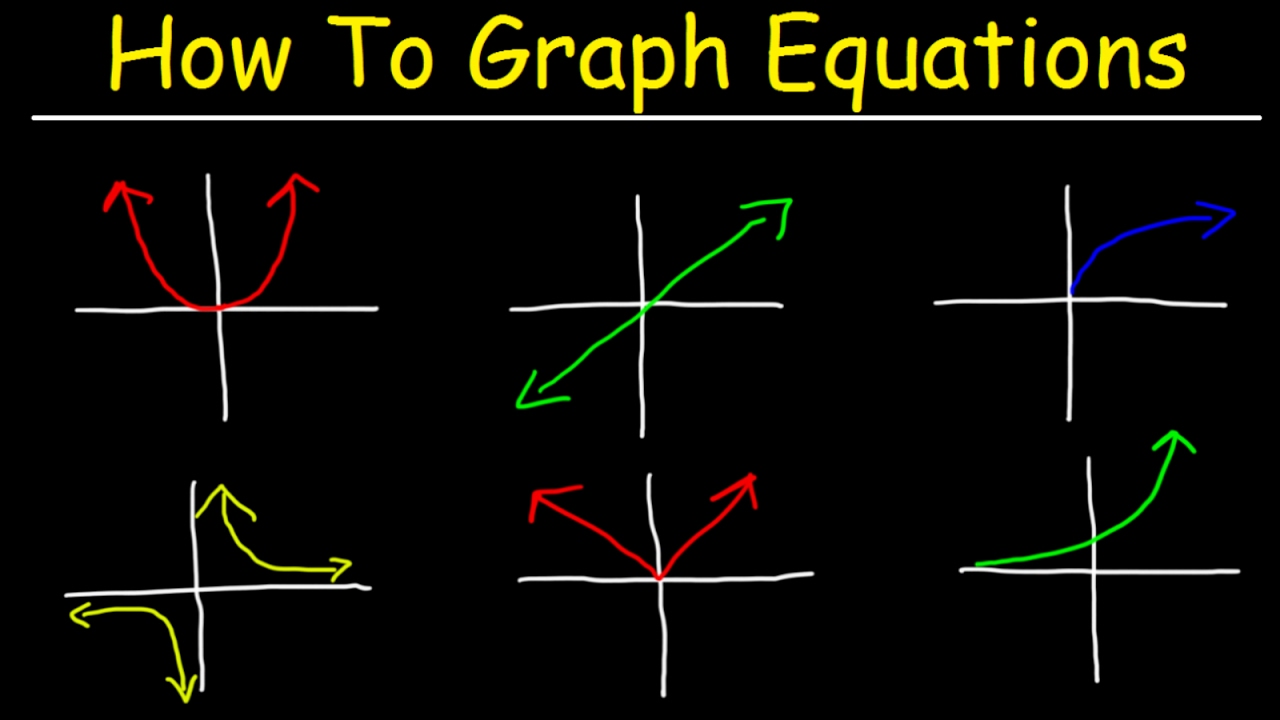
The very essence of a function finds its expression in its graphical form. The shape a graph takes is not arbitrary; it's a direct reflection of the function's intrinsic nature. A linear function, for instance, dictates a straight-line graph, its trajectory precisely determined by its slope and intercept. These elements dictate its movement across the Cartesian plane. Conversely, a quadratic function, characterized by its squared variable, unveils itself as a 'U'-shaped curve, or parabola, opening upwards or downwards based on the sign of its leading coefficient. Trigonometric functions, such as sine and cosine, paint a different picture entirely, their graphs undulating in a mesmerizing, wave-like pattern, oscillating between peaks and troughs. Even the absolute value function has its own signature, with its graph taking the form of a 'V', a testament to the inherent properties of the absolute value operation.

Understanding these basic graph types provides a foundation for exploring more complex functions. Take, for example, the cardioid, a captivating curve that resembles an apple without a stem, its name stemming from the Greek word for "heart". This elegant form arises from the movement of a point on the perimeter of one circle as it rolls around another. Because manually sketching the curve is difficult, it is easier to use a graphing mechanism.

Beyond these fundamental shapes, various types of graphs are indispensable tools in the mathematical arsenal. You must be able to recognise, sketch, and interpret the following graphs:

Linear graphs, such as y = mx + b
Quadratic graphs, such as y = ax + bx + c
Cubic graphs
Reciprocal graphs

Consider a linear graph, produced by a linear function represented by the equation {eq}y=mx+b {\/eq}. The line's steepness is dictated by the slope, 'm', while 'b' determines where the line intersects the y-axis. Another specific example is a constant function; its graph is a horizontal line, meaning the function's value remains constant, regardless of the value of x. In the realm of polar equations, the approach to graphing alters. These equations use radius and angle coordinates, and testing for symmetry across the line \$\\theta=\\dfrac{\\pi}{2}\$, the polar axis, or the pole simplifies the graphing process.

Before we delve deeper, here's a table showing the essential characteristics of different graph types:

Graph Type	Equation Form	Typical Shape	Key Features
Linear	y = mx + b	Straight line	Slope (m), y-intercept (b)
Quadratic	y = ax + bx + c	Parabola (U-shaped)	Vertex, axis of symmetry, x-intercepts (roots)
Cubic	y = ax + bx + cx + d	S-shaped curve (can vary)	Inflection points, x-intercepts (roots)
Reciprocal	y = k/x (and variations)	Hyperbola	Asymptotes, domain restrictions
Sine/Cosine	y = sin(x), y = cos(x)	Wave-like	Amplitude, period, phase shift
Absolute Value	y = \|x\|	V-shaped	Vertex (point)

You might also find these helpful to understand more:

Maths is Fun - Equation of a Line
Khan Academy - Graphing Quadratic Functions

To accurately sketch a graph of an equation, it's crucial to master a few key techniques. The first step is to pinpoint the type of function, which is best done by observing the graph's overall shape. Then, by choosing several strategic points on the graph and applying the function's general equation, you can derive the precise equation. Another efficient method is to plot various points for the equation. The reciprocal graph, which appears as two branches that never touch the axes. Shifting and transforming graphs offers an additional layer of understanding; shifting a graph involves changing its position. The vertical shifting of a graph is shown by changing the constant within the equation.

Let us now explore the process of sketching a graph of an equation. The procedure generally involves plotting several points to gain an understanding of the function's behaviour. The key steps are as follows:

Identify the Equation: Determine the function's equation (e.g., y = x + 2x + 1)
Create a Table of Values: Select a range of x-values (e.g., -3, -2, -1, 0, 1, 2, 3) and calculate the corresponding y-values by substituting the x-values into the equation.
Plot the Points: Use the table of values to plot the (x, y) coordinates on a graph.
Connect the Points: Draw a smooth curve through the plotted points. The shape of the curve will depend on the type of function (e.g., a parabola for a quadratic equation, a straight line for a linear equation).

Now, let's examine some applications. The intersection of graphs can provide solutions to equations. In fact, we use them to solve equations relating to the graph. When two or more equations are graphed on the same coordinate plane, their points of intersection represent the solutions that satisfy all equations simultaneously. Furthermore, consider the graph of an equation as it relates to real-world phenomena. For example, the graph of benefits given to the people, if in year 2002 a total of 6 million people received benefits, then that point will be considered as a vertex on the graph.

A function of the form f(x) = mx + b describes a linear function. The graph of this function is a straight line. The "m" represents the slope. And "b" determines the y-intercept. Another type of linear function is a constant function. It is a horizontal line, where f(x) always equals a constant value.

Now, we'll look at different types of graphs and how to interpret them.

The graph of a quadratic function is 'U' shaped, or parabola.
The graph of the sine/cosine function is wavy.
The graph of an absolute value function is 'V' shaped.

Here are some of the most commonly used functions, and their graphs:

f(x) = mx + b

There are many equations associated with a particular type of graph. Let's look at some examples to understand this better.

(4) is a reciprocal equation with a positive coefficient so matches graph b
(5) is a quadratic equation with a negative coefficient so matches graph c
(2) is the only equation not yet used, so by elimination it is graph a.
Graph a equation 2.
Graph b equation 4.
Graph c equation 5.
Graph d equation 1.
Graph e equation 3

Now consider the basic transformations that are often used in graphing functions.

A reciprocal graph can be represented as a formula, where a and b are constants.
The shape of this graph will remain the same.
But if is shifted upwards by units.
Would be shifted down by 3 units.
This means the horizontal asymptote also shifts up by units

Recognising graphs is a vital skill in mathematics, essential for the GCSE exam and beyond. These graphs serve as visual representations of algebraic relationships, offering insights into functions, equations, and data trends. For students, the process of sketching these graphs involves plotting points, understanding key features, and grasping the impact of transformations. Recognizing graphs entails the ability to interpret equations and to match them accurately with their corresponding graphical forms.

There are many resources to get you started, including understanding higher level functions and their graphs. Here you can find: linear, quadratic, cubic, and reciprocal graphs. The ability to recognize, sketch, and interpret these graphs is a cornerstone of mathematical proficiency. Graphs make it possible to understand complex equations.

The following is a list of key graph types you need to understand:

Linear
Quadratic
Cubic
Reciprocal

For each graph type, it's essential to grasp its defining characteristics:

The equation form
The typical shape
Key features.

The quadratic graph is one of the most essential functions, characterised by a 'U' shape. The general equation for a quadratic graph is y = ax + bx + c. The direction of the parabola (whether it opens upwards or downwards) depends on the sign of the coefficient 'a'. If 'a' is positive, the parabola opens upwards; if 'a' is negative, it opens downwards. The term 'b' influences the position and orientation of the parabola. The constant 'c' determines the y-intercept, the point at which the graph intersects the y-axis.

For example, in the equation y = 2x + 3x + 4, the coefficient of x is positive (2), indicating that the parabola opens upwards.

When sketching the graph of an equation, begin by identifying the type of function. This will guide the process. For a quadratic function, plotting points is important. After plotting various points for the equation, connect them with a smooth curve to form the parabola. Remember that symmetry often helps; a parabola is symmetrical about its axis of symmetry, which can aid in accurate sketching. To accurately sketch a graph of an equation, it's crucial to master a few key techniques.

In the field of polar coordinates, it is easier to graph polar equations if we can test the equations for symmetry with respect to the line \$\\theta=\\dfrac{\\pi}{2}\$, the polar axis, or the pole. There are three symmetry tests that indicate whether the graph of a polar equation will exhibit symmetry. If an equation fails a symmetry test, the graph may or may not exhibit symmetry. Sketching a quadric surface is best approached by first understanding its basic properties. You can understand this better by graphing these yourself. Lets try graphing $\\dfrac{x^2}{4} + \\dfrac{y^2}{16} + \\dfrac{z^2}{9} = 1$ first.

By combining the above understanding and insights, you will be able to understand graphs, and their equations. Remember that it takes time and practice to fully understand and implement the principles of graphing. Continue practicing, learning new equations, functions, and graphs to gain a deeper understanding of the math principles.