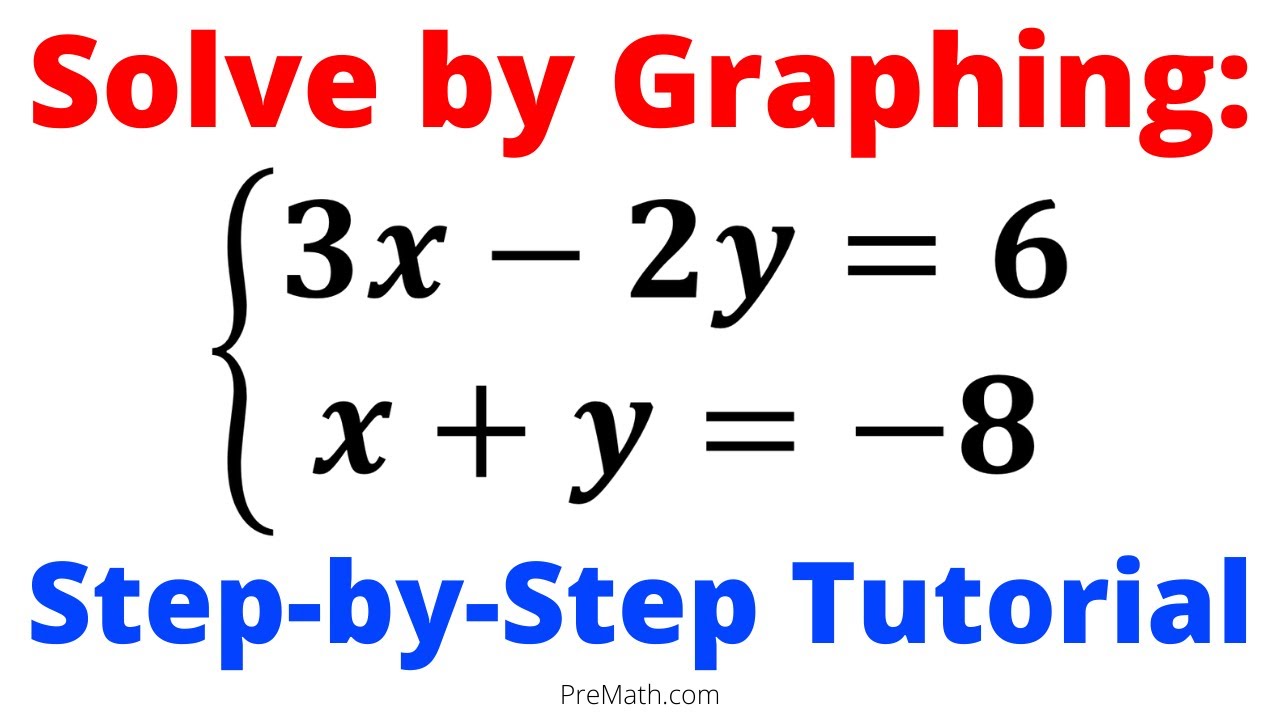Can the seemingly simple act of drawing lines on a graph unlock the mysteries hidden within a complex system of equations? Indeed, graphing provides a visually intuitive, albeit sometimes less precise, method for deciphering the solutions to these mathematical puzzles.

The world of mathematics often presents us with intricate problems that require systematic approaches. One such challenge lies in the realm of systems of equations, a set of two or more equations sharing the same unknown variables. Solving these systems, whether they involve linear or non-linear equations, is a fundamental skill with wide-ranging applications in various fields, from engineering and economics to computer science and everyday problem-solving. While multiple methods exist for tackling these systems, graphing stands out as a particularly accessible and visually engaging technique, especially for those new to the concepts. This article delves into the art of solving systems of equations by graphing, providing a clear and comprehensive understanding of the process.

Let's explore the mechanics of this graphical approach. The core principle rests on the graphical representation of each equation within the system. The graph of a linear equation, as many of us recall, is a straight line. Every single point residing on this line represents a solution to that specific equation. Thus, for a system of two equations, we're essentially plotting two lines on the same coordinate plane. The point where these lines intersect holds the key it's the ordered pair (x, y) that satisfies both equations simultaneously. This intersection point is, therefore, the solution to the system.

The fundamental concept of using a graphing calculator to solve systems of equations is remarkably straightforward. The academic center for excellence published content of this method on February 1, 2024, and it remains a widely utilized method, providing a practical and accurate approach to solving these systems. The initial step involves converting the equations into a form conducive to graphing on a calculator: the y = form. This means isolating the variable 'y' on the left side of the equation, ensuring that the right side contains the remaining terms and constants. For example, if you have an equation like 2x + y = 5, rearranging it to y = -2x + 5 makes it graph-ready.

The visual nature of graphing makes it particularly well-suited for understanding the nature of solutions. When the lines intersect at a single point, the system is considered consistent, and it possesses a unique solution the coordinates of that intersection point. However, the graphical method also illuminates other possibilities. If the graphed lines are parallel, they will never intersect. In this case, the system is inconsistent, indicating that no solution exists that satisfies both equations. Finally, if the two equations are essentially equivalent, meaning they represent the same line, the system is consistent and possesses an infinite number of solutions. Each point on that single line represents a valid solution.

Before diving into the mechanics of graphing, it's important to understand the types of systems of equations we might encounter. A linear system is one where all the equations within the system are linear, meaning that the variables are raised to the power of one. The graph of each equation in such a system will be a straight line. Non-linear systems, on the other hand, contain at least one equation that is not linear, often involving variables raised to powers other than one or including other mathematical functions. These systems can give rise to curved graphs, such as parabolas or circles. The method of solving these is the same in essence, but the lines will take new shapes. Another consideration is the number of variables. While this article predominantly focuses on systems with two variables (typically x and y), the concepts extend to systems with more variables, though the graphical representation becomes more complex.

The core steps involved in solving a system of equations by graphing are relatively simple but require careful execution. First, transform each equation in the system into the slope-intercept form (y = mx + b) if it isn't already. This form allows for easy identification of the slope (m) and the y-intercept (b), making graphing straightforward. Next, using either graph paper or a graphing calculator, plot each equation on the same coordinate plane. This can be done manually by calculating a few points on each line and connecting them, or by utilizing the calculator's graphing function. Finally, identify the point of intersection of the graphed lines. The coordinates of this point represent the solution to the system of equations. If the lines are parallel or coincide (the same line), the system is either inconsistent or has infinite solutions, respectively.

To better appreciate the application of graphing to solve a system of equations, let's consider a few practical examples. Solving these systems of equations by graphing is a skill that is typically introduced in the 8th grade when students learn linear systems, providing them with their first exposure to solving multiple equations at once.

Let us consider a scenario:

Example 1: A system of two linear equations, where two equations can be made based on how far two runners have ran.

Here, the two equations would be:

Equation 1: d = 0.2t (runner one)

Equation 2: D = 0.5(t-6) (runner two)

Here, we would be finding the distance, given d as the distance and t as the time in minutes. As illustrated by the example, graphing can be used to solve real-world application problems and provide a practical approach to answering such questions.

The ability to graph equations, particularly linear equations, is fundamental to this process. Mastering this skill allows one to tackle a wide range of problems, from basic mathematical exercises to more complex real-world scenarios. Students in 8th grade typically start to encounter these types of problems, learning to apply their new skills to solve a variety of practical questions.

Consider a more concrete example:

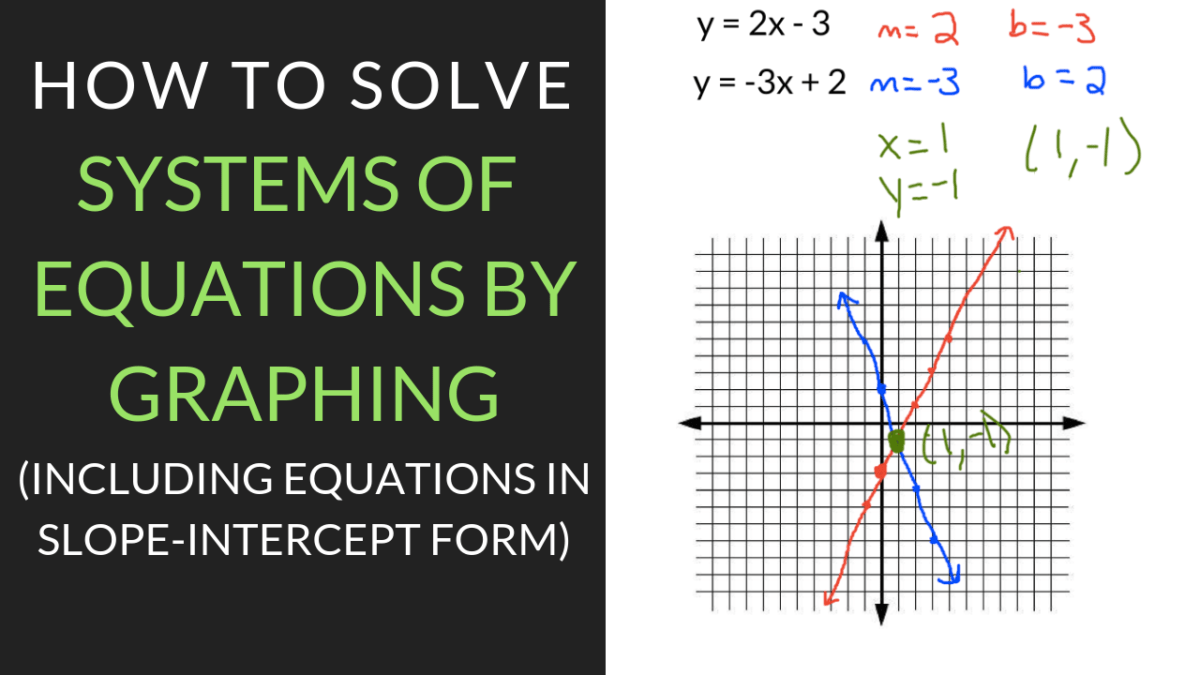
Example 2: Solve the system of equations:

y = 2x + 1

y = -x + 4

To solve by graphing, we would proceed as follows:

Graph the equations: Since both equations are already in slope-intercept form (y = mx + b), we can readily graph them. For y = 2x + 1, the slope (m) is 2, and the y-intercept (b) is 1. For y = -x + 4, the slope is -1, and the y-intercept is 4. Plotting these lines on the same coordinate plane.
Find the intersection: Observe where the two lines intersect. In this case, the lines intersect at the point (1, 3).
Solution: The solution to the system of equations is x = 1, y = 3. This means the point (1, 3) is the only point that satisfies both equations simultaneously.

Another Example:

Example 3: Consider a system of equations, where one of the runners gets a head start, while the other is running slightly faster.

The equations can be as follows:

y = 0.2x (the first runner)

y = 0.5(x-6) (the second runner)

By graphing these equations, we can find out when the faster runner overtakes the slower one, and at what distance. These concepts can be used to solve real-world application problems that are modeled by a system of equations.

Analyzing the form of each equation in the system is another vital step. Does the equation readily lend itself to graphical representation? Is it already in slope-intercept form? Or, does it require manipulation to isolate 'y'? Answering these questions helps streamline the graphing process. If an equation isn't in a graphing-friendly form, rearranging it to y= form is often the first action.

Graphing calculators are invaluable tools in the context of solving systems of equations. They automate the process of graphing, allowing for quick and accurate visualizations. Most graphing calculators have built-in functions that facilitate entering equations in various forms, displaying the graphs, and even identifying the point of intersection. Using a graphing calculator provides an immediate view of the solution, saving time and minimizing computational errors. To use a graphing calculator effectively, you typically enter the equations, set an appropriate viewing window (x and y ranges), and then utilize the calculator's "intersect" function to find the point of intersection.

However, graphing isn't the only method for solving systems of equations. Alternative techniques include substitution and elimination. Substitution involves solving one equation for one variable and then substituting that expression into the other equation. Elimination entails manipulating the equations to eliminate one of the variables, resulting in a single equation with one variable, which can then be readily solved. Each method possesses its own advantages and disadvantages, making it a valuable skill to be familiar with. Depending on the nature of the equations, one approach may prove more efficient or straightforward than the others. Furthermore, understanding multiple methods provides a deeper comprehension of the underlying concepts.

Regardless of the chosen method, it's essential to verify the solutions obtained. Substituting the calculated values of x and y back into the original equations provides a simple way to check if the solution satisfies both equations. This step helps identify any potential errors in the calculation or graphing process and assures that the obtained solution is valid. For example, if you solve the system y = 2x + 1 and y = -x + 4 by graphing and get the point (1, 3), substitute x = 1 and y = 3 into both equations, verifying that 3 = 2(1) + 1 and 3 = -(1) + 4, confirming that (1, 3) is indeed the solution.

Furthermore, consider the nature of the solution itself. Is it a single point, indicating a unique solution? Or are the lines parallel, indicating no solution? Or do the lines coincide, leading to an infinite number of solutions? Each of these possibilities has a distinct implication, offering insights into the relationship between the equations within the system. Inconsistent systems provide no shared solutions, while dependent systems share an infinite number of shared solutions. When encountering parallel lines, recognize that there is no intersection, representing an inconsistent system without a shared solution. If the equations represent the same line (coincident), the system is dependent, where the solutions are infinite.

In the realm of solving systems of equations, understanding that multiple methods exist is essential. Besides graphing, algebra techniques offer approaches such as substitution and elimination. A system of equations is essentially a collection of two or more equations, and the solution is the values that satisfy them. While graphing is a great visual tool, algebra, and other techniques help give another perspective on understanding these systems of equations. Understanding the various approaches to solving these types of equations gives the solver a variety of tools to address complex and potentially interesting problems.

The application of these concepts extends beyond academic exercises. Systems of equations are used to model numerous real-world scenarios. These can tell you when one contestant will overtake another who has a head start, as in a boating race or marathon. For instance, in economics, systems of equations can model supply and demand curves to determine market equilibrium. In physics, they can describe the motion of objects under the influence of multiple forces. The ability to translate real-world problems into mathematical models and then solve them is an important skill. Solving a system of linear equations is important, and it can be applied to many situations in various real-world situations.

Finally, consider the role of technology in solving systems of equations. Graphing calculators and dedicated software offer streamlined solutions. These tools not only aid in graphing but also provide accurate solutions and offer the potential to work with more complex systems of equations. However, it is important to cultivate a strong fundamental understanding of the concepts, as technology should serve as a tool to facilitate and amplify problem-solving skills, rather than supplanting the ability to understand the underlying mathematics. The goal is to utilize good algebra techniques. Remember to always check the answer in the problem to make sure it makes sense, and the question with a complete sentence.