Do you know the subtle yet significant difference between a function and a simple equation? Functions, unlike equations, are meticulously designed to establish a unique relationship between inputs and outputs, making them a fundamental concept in mathematics and various scientific fields.
Functions and equations, though often intertwined, serve distinct purposes in expressing mathematical relationships. An equation, at its core, simply illustrates a relationship between variables. For instance, an equation might express how the price of a product relates to its quantity. However, it doesn't inherently dictate the dependency or independence of those variables. A function, on the other hand, goes a step further. It defines a specific rule or process that transforms one input value (the independent variable, often denoted as 'x') into a unique output value (the dependent variable, typically 'y').
Functions are frequently represented using equations. This is achieved through what is known as function notation. For example, we might use 'f(x)' to denote a function, where 'f' is the function's name, and 'x' is the input variable. This notation clearly signifies that the function 'f' operates on the input 'x' to produce an output.
- Khatrimazain Your Ultimate Destination For Movie Downloads And Entertainment
- Bollywood Bollyflix Your Ultimate Guide To Streaming Indian Cinema
The essence of a function lies in its ability to produce a single, definite output for every given input. This "uniqueness" is what separates functions from broader equations. Consider the equation 4p + 3q = 7. While this equation shows a relationship between 'p' and 'q', it does not impose any requirement that one variable be the independent and the other the dependent. However, when an equation is cast as a function, such as y = f(x), the role of 'x' as the input and 'y' as the output becomes explicit.
Understanding the difference between functions and equations opens doors to advanced mathematical concepts. Mastering these concepts is crucial, with an understanding of algebra playing a pivotal role.
Consider the following table, which highlights the key contrasts:
- Hdhub4u Go Your Ultimate Guide To Streaming Movies And Tv Shows
- Exploring The World Of Mydesi49net Your Ultimate Guide
| Feature | Equation | Function |
|---|---|---|
| Purpose | Expresses a relationship between variables. | Defines a unique relationship between inputs and outputs. |
| Variables | Variables are related, but roles (independent/dependent) are not necessarily defined. | Clearly defines independent (input) and dependent (output) variables. |
| Output | May or may not have a unique output for a given input. | Guaranteed to have a unique output for every input. |
| Notation | Various forms, e.g., 4p + 3q = 7. | Utilizes function notation, e.g., f(x) = y. |
To delve deeper into the specifics of functions and their equation-based representations, the online resources provided by Khan Academy offer invaluable support. The site is a well-renowned provider of educational content and offers a wealth of information regarding functions and related topics.
Let's explore the world of functions. These are not limited to simple equations. They can be visualized using graphs, tables, and even described in words. The beauty of a function lies in its versatility.
Equations, graphs, tables, or words can represent functions. However, a function expressed as an equation is typically denoted using what's called function notation. For example, 'f' might be the name of the function. When it comes to two variables, equations can often be expressed as functions using function notation. The variable that can change, or 'x,' is the independent variable. Different letters can be used to name functions. The key difference between an equation and a function is that functions link each value of the independent variable to a unique value of the dependent variable.
The independent variable represents the input values, while the dependent variable represents the output values determined by the function's rule. While an equation always shows a relationship between variables, the relationship is not necessarily viewed as a function with independent and dependent variables. In the equation 4p + 3q = 7, there is no requirement for one variable to be independent and the other dependent.
An equation in two (or more) variables can sometimes be solved in terms of one of the variables. This type of equation is closely related to the notion of a function.
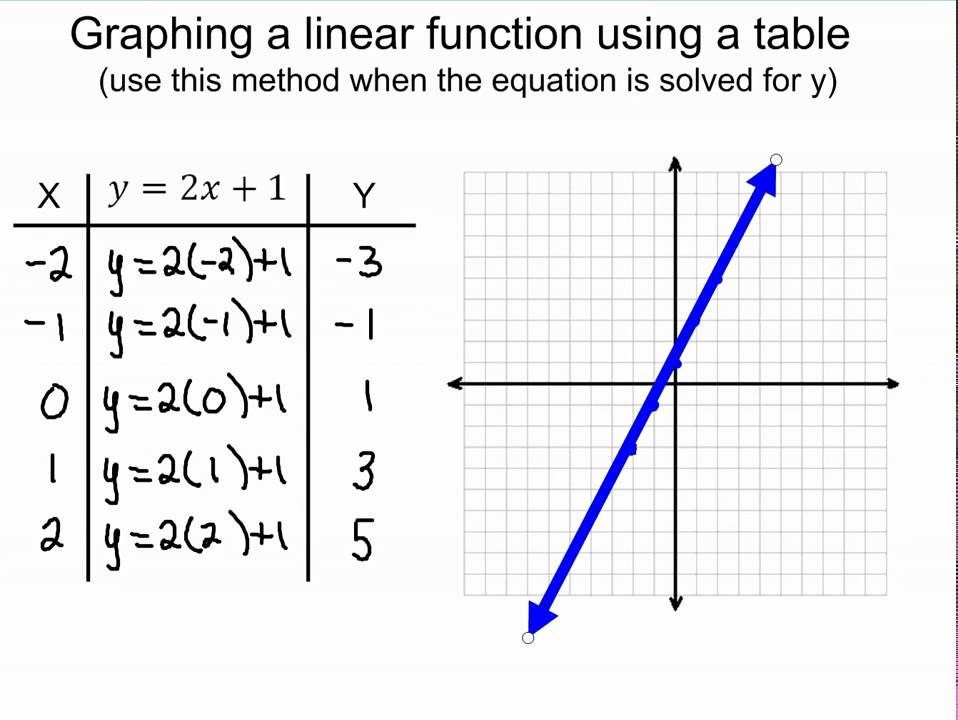
Let's consider another example: a simple equation such as y = 2x + 3. This is a function, and we can write it in function notation as f(x) = 2x + 3. Here, 'x' is the input, '2x + 3' is the rule, and the value of 'y' is the output. For every value of 'x', there is only one value of 'y'.
There's a vast array of functions in mathematics. The squaring of a number (x2) is a function. So is x3 + 1. Trigonometric functions, such as sine, cosine, and tangent, are also functions. Many more examples exist, underscoring the pervasiveness of functions in mathematical applications.
When converting between expressions and functions, it's crucial to know how to navigate the two forms. Some software tools may work only with either functions or expressions. Converting from a function to an expression is simple; when 'f' is a function, then f(x) is the expression obtained by applying 'f' to the variable 'x'.
Some functions are defined by mathematical rules or procedures expressed in equation form. If it is possible to express the function output with a formula involving the input quantity, then we can define a function in algebraic form. For example, the equation [latex]2n+6p=12[\/latex] expresses a functional relationship between [latex]n[\/latex].
Equations and inequalities come to life through graphs, tables, and even words, providing different perspectives on their behaviour.
Functions are the building blocks of calculus, the language of change. Understanding them is crucial for grasping concepts such as limits, derivatives, and integrals. These concepts are fundamental to physics, engineering, economics, and many other disciplines.
Functions find application in modelling real-world phenomena. Whether predicting the trajectory of a projectile, or analyzing the growth of a population, functions serve as powerful tools.
Consider a scenario. You might want to calculate the total cost of buying apples. Let 'x' represent the number of apples, and 'C(x)' represent the total cost. If each apple costs $0.50, the function can be written as C(x) = 0.50x. This function allows you to find the total cost for any number of apples by simply substituting the number of apples into the function.
Equations can be categorized and grouped based on complexity and the operations involved within the equation.
To solve equations, we can utilize different techniques. Logarithmic equations, for example, can be converted from exponential form. For equations involving multiple logarithms, logarithmic properties come into play. The aim in solving is always to isolate the variable on one side of the equation.
Several online resources can assist you in solving equations. Linear equation calculators, for example, allow users to input equations, and the calculator does the calculations. These calculators can handle equations with one or two variables.
Linear equations are an important subset of the broader category of equations. They are represented graphically by straight lines. A linear equation can be solved using a variety of methods, including algebraic manipulation, substitution, and elimination.
The world of trigonometric equations expands the scope further. Trigonometric equations involve trigonometric functions such as sine, cosine, and tangent. Similar to polynomial or rational equations, solutions are specific values of the variable.
Mastering functions and equations is a journey, and the path is paved with practice. From basic algebraic expressions to advanced calculus concepts, a strong foundation in these concepts is essential for any student. With dedication, and a little patience, anyone can navigate the mathematical landscape and unveil its profound beauty.
Always remember the key difference: a function assigns each input to precisely one output, while an equation may show a relationship without this uniqueness. Once you grasp this fundamental distinction, you will be well on your way to understanding more complex mathematical concepts.
If you're looking for resources to help you learn more, try the interactive exercises and videos on Khan Academy. Solving more complex equations is simplified with tools such as a linear equation calculator.
By recognizing the distinction, you can successfully navigate the realm of math, unlocking its power and making its beauty your own. Remember, whether in solving for an unknown in an equation or examining a function, understanding both will empower your analytical skills.
- Bolliflix Your Ultimate Guide To Streaming Bollywood Movies
- Ivo Graham Carrie Matthews The Story You Need To Know