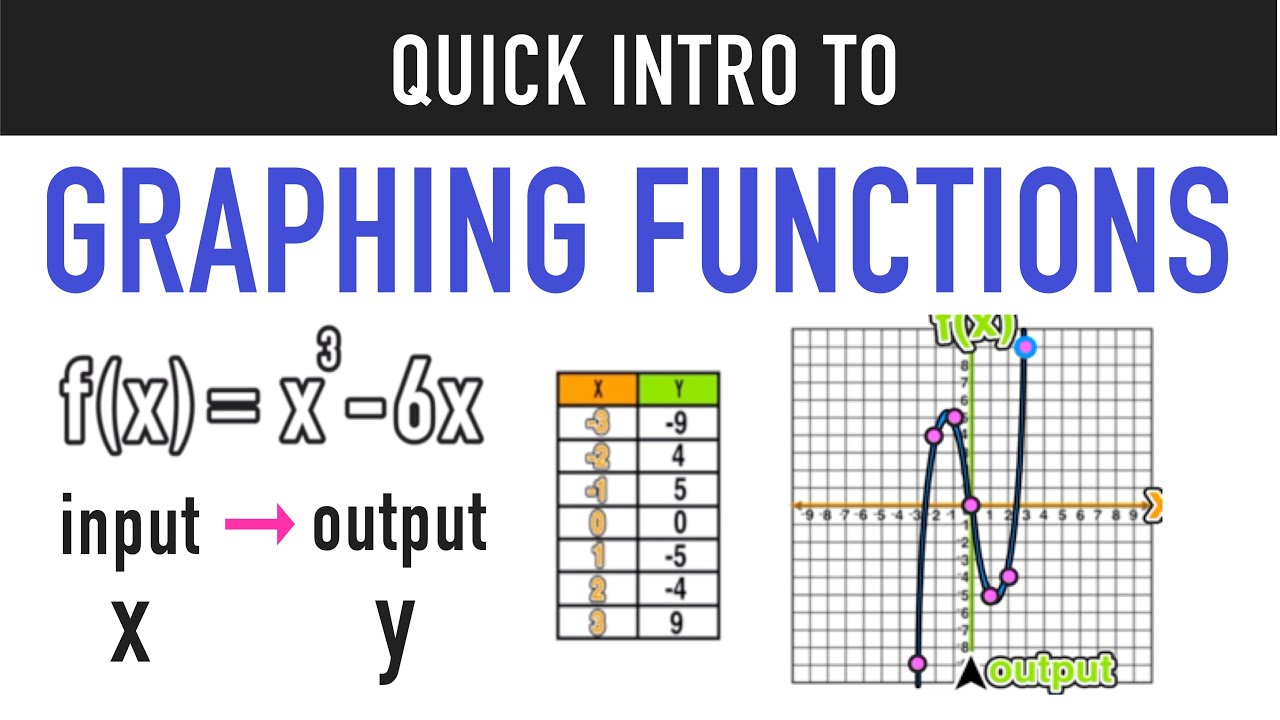
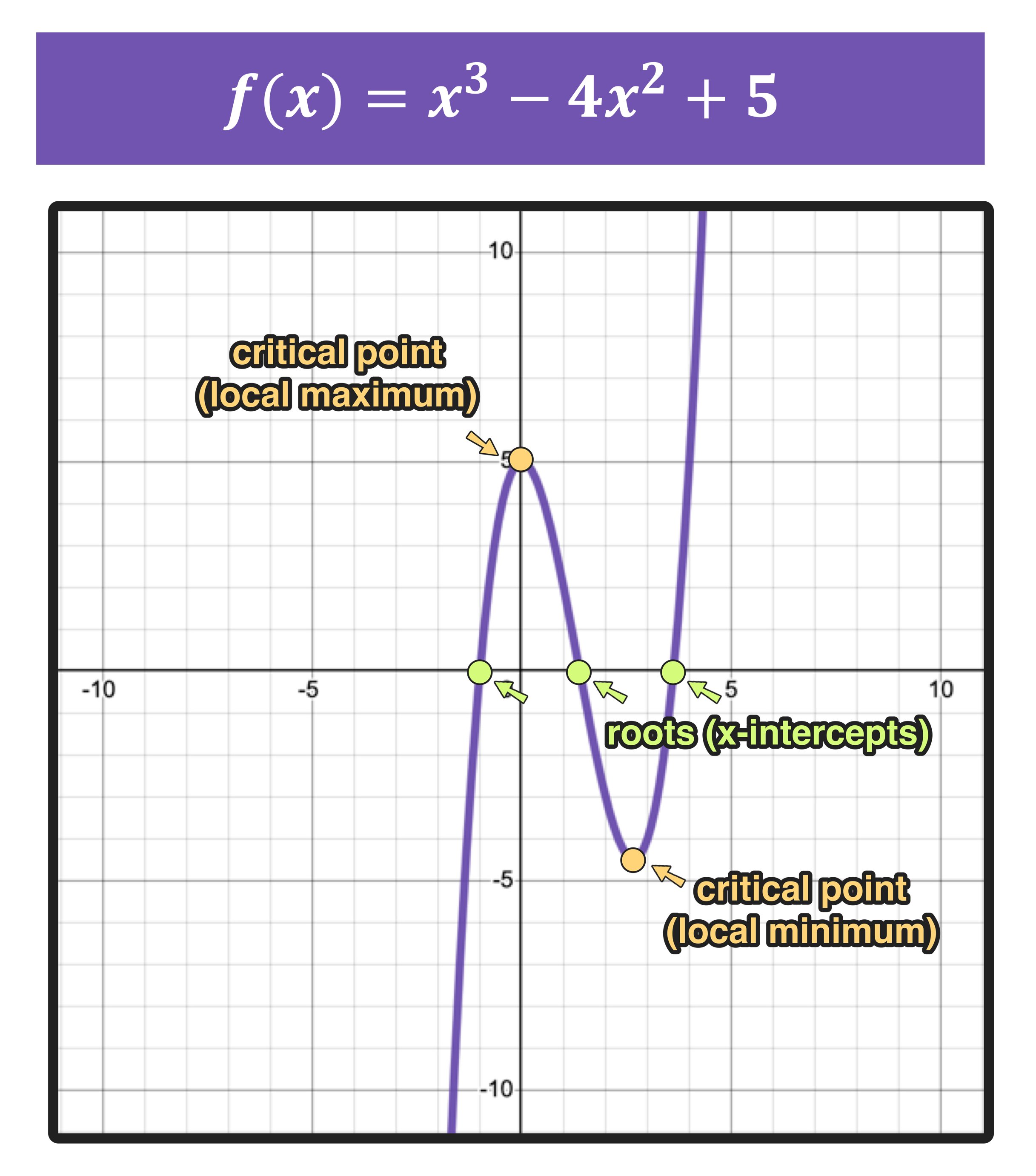
How does one truly visualize the often abstract world of mathematical functions? The ability to graph a function is not merely a skill; it is a gateway to understanding the very nature of mathematical relationships, making complex concepts tangible and accessible.

From the fundamental building blocks of algebra to the intricate landscapes of calculus, the ability to represent functions graphically unlocks a deeper comprehension. Imagine transforming equations, those sometimes intimidating strings of symbols, into visual narratives that tell a story of change, relationships, and patterns. This skill is not just about plotting points; it's about converting a world of numbers into visual information.

Concept	Description	Details
Function Definition (Set Theory)	A function, from a set x (the domain) to a set y (the codomain), is defined by its graph.	The graph of a function is a subset of the Cartesian product (x y), containing ordered pairs (x, y) where each x in the domain is paired with a unique y in the codomain. Formally, a function is a triple consisting of the domain, codomain, and its graph.
Graph of a Function	The visual representation of a function's relationship between input (x) and output (y).	The graph provides an immediate visual of how the output changes as the input varies. It shows the complete behavior of the function.
Domain	The set of all possible input values (x-values) for a function.	These are the values for which the function is defined, and it is from this set that we take values to input into the function.
Codomain	The set of all possible output values (y-values).	The range of the function is a subset of the codomain, this is the actual set of output values that can be obtained from the function.
Cartesian Product	The set of all possible ordered pairs formed by taking an element from set x and an element from set y.	The Cartesian product of two sets A and B, denoted by A B, is the set of all ordered pairs (a, b) where a belongs to A and b belongs to B.
Graphing Tools	Resources that are used to help visualize functions and equations	Online graphing calculators like GeoGebra and WolframAlpha and other are popular and allow plotting, visualization of algebraic equations and animating graphs
Vertical Line Test	A visual method used to determine if a graph represents a function.	If any vertical line intersects the graph at more than one point, the graph does not represent a function.
Points of Intersection	The points where two or more graphs intersect.	Graphing multiple functions together, such as g(x) = x^2 + 1, highlights the intersection of the curves.
Function Notation	The standard way of representing functions, such as f(x).	f(x) denotes a function "f" of x, and what is put inside the parentheses (e.g., x) represents the input to the function.
Linear Function	A function whose graph is a straight line.	A simple example is f(x) = x+3.
Rational Function	A function that can be expressed as the quotient of two polynomials.	Graphing rational functions often involves analyzing asymptotes and discontinuities.
Greatest Integer Function	A function that returns the greatest integer less than or equal to the input value.	Also known as the floor function, denoted f(x) = [x].

Reference website (Mathsisfun.com)

The process of graphing functions, however, isn't merely a rote exercise of plugging numbers into an equation; it is a dynamic interaction that builds a bridge between abstract equations and tangible visualizations.

Let's begin with the essentials. To graph a function effectively, one must grasp the fundamental principles. The basis lies in understanding that a function maps elements from a set (the domain) to another set (the codomain). The graph of the function itself is a subset of the Cartesian product of these two sets. But what does this mean in practical terms? In essence, it describes the relationship between the function's inputs (x-values) and its outputs (y-values).

A function is often denoted as f(x), where 'f' is the function's name, and 'x' represents the input. The beauty of function notation lies in its ability to encapsulate mathematical processes in a concise, universally understandable way. For instance, f(x) = x + 3 dictates that for every input 'x', the function adds three to it. Similarly, f(x) = x shows us that the function squares the input 'x'.

The first step, no matter the function, is to enter the function's formula into a graphing tool or plotting it by hand. Tools such as Wolfram Alpha, GeoGebra, and countless others facilitate this. Simply type the equation into the designated area, and the tool instantly generates a graphical representation. For hand plotting, you can select a range of x-values, compute the corresponding f(x) values, and plot these pairs as points on a coordinate plane.

For a linear function, such as the simple f(x) = x + 3, the graph will be a straight line. To plot this, select several x values (0, 1, 2 for example). Substitute each value into the function equation to get the corresponding y value (3, 4, 5 respectively). Plot these points (0,3), (1,4) and (2,5) on a graph. Then, draw a straight line through these points. The line represents all points on the graph of the function.

The vertical line test is a useful tool. If a vertical line can be drawn anywhere on the graph, and only touches the graph at a single point, then the graph does represent a function. If it intersects the graph at more than one point, the relationship is not a function.

Graphing more complex functions, such as the rational function or the greatest integer function, requires a bit more finesse. Rational functions, defined as the ratio of two polynomials, may have asymptotes and points of discontinuity, which require a more detailed analysis.

Consider the graph of a rational function. The first step is to identify any points where the function might be undefined (e.g., where the denominator equals zero). These points often result in vertical asymptotes. Plot the asymptotes as dashed lines to prevent the graph from intersecting them. Find other points such as roots where the function intersects the x-axis. The next step is to analyze the behavior of the function as x approaches positive and negative infinity. Plotting these points, combined with a thorough understanding of asymptotes, will yield a more accurate and comprehensive graphical representation.

Graphing the greatest integer function, sometimes called the floor function, presents a different challenge. This function, denoted f(x) = [x], returns the greatest integer less than or equal to x. For every interval between two consecutive integers, the graph consists of a horizontal line. This creates a stepped, staircase-like appearance. For instance, from x=0 to x=1, the function output remains 0. However, at x=1, the output jumps to 1.

Online graphing tools are indispensable for learning. They allow you to experiment with different functions, visualize changes as you adjust variables, and understand the principles more intuitively. Use these tools actively. Input various functions, alter them, and observe how the graphs change. These interactive experiences cement understanding more effectively than passive reading alone.

When working with graphs, one of the most common practices is identifying the points of interest. Some tools allow you to select a curve and view the intersection points. These points are often critical in solving problems, for they represent where the function has a specific value. By selecting the curve on the graph or its expression line, one can find these points.

Visualizing equations and functions through interactive graphs and plots offers a new level of insight, especially when exploring functions with multiple dimensions.

Plotting and graphing are ultimately methods of visualizing the behavior of mathematical functions. Wolfram Alpha is an excellent tool for generating plots of functions, equations, and inequalities in one, two, and three dimensions. It allows the user to generate polar plots, parametric plots, contour plots, and region plots. Using these tools and the method of graphing mentioned above, the user can have better insight into the functions being used.

Mastering function graphing is not just a crucial mathematical skill, it unlocks a new way to look at the world. Graphing is how we connect abstract ideas to visual representations, and that is the true power of this skill. Through this understanding, one can effectively read data that is collected from the real world and create meaningful interpretations.