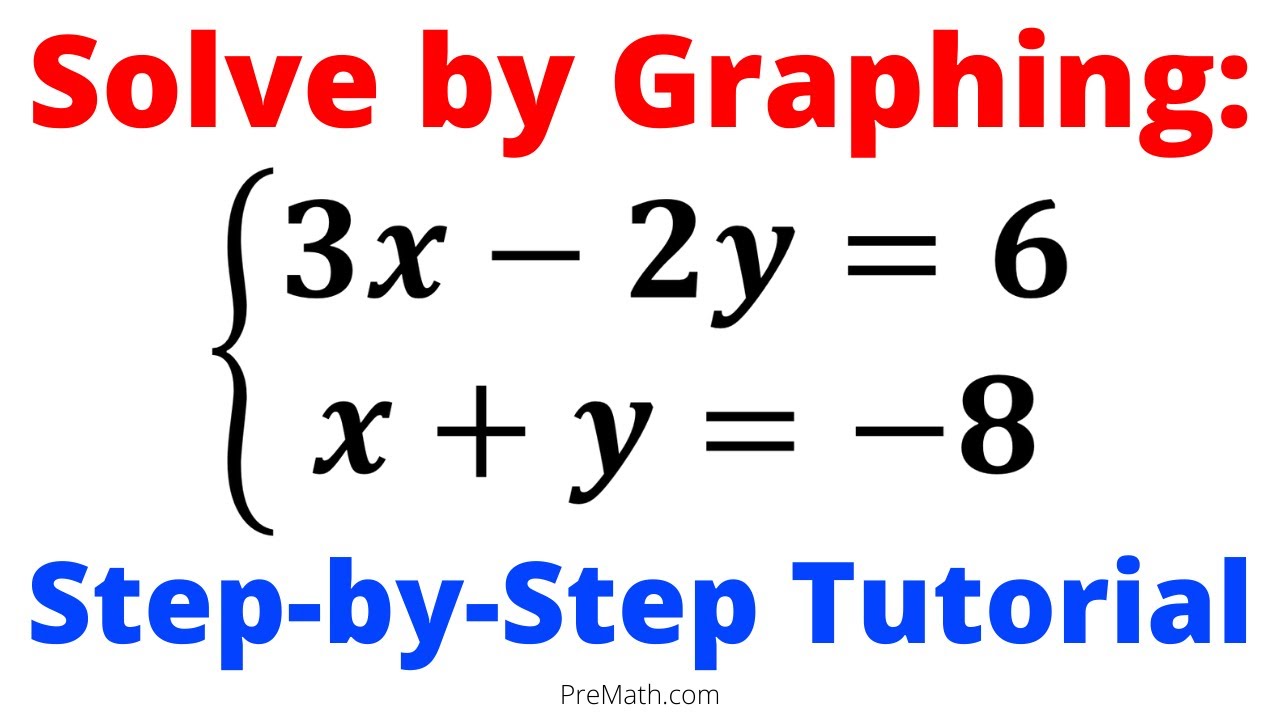Learn To Solve Systems Of Equations: Methods & Examples

Ever found yourself wrestling with equations, feeling like you're navigating a maze of numbers? Understanding and mastering systems of equations is not just a mathematical exercise; it's a gateway to problem-solving skills applicable in virtually every aspect of life.

The journey into the world of systems of equations is a fascinating one. It's about uncovering the hidden relationships between multiple equations, each potentially representing a different aspect of a problem. Solving these systems allows us to pinpoint the exact values that satisfy every equation simultaneously, revealing a comprehensive solution.

At their core, systems of equations are a collection of equations, each sharing one or more variables. The objective is to discover the values of these variables that render every equation in the system true. This ability to find common ground, to identify the single point where multiple conditions converge, is what makes solving systems of equations such a vital skill.

• Somali Wasmo Telegram 2025 The Ultimate Guide To The Rising Trend
• Unpacking The Mysterious World Of Masa49 Org A Comprehensive Guide

There are primarily three ways to solve systems of equations manually: the substitution method, the elimination method, and graphing. Each technique offers a different approach to finding the solution, and the ideal method often depends on the specifics of the equations themselves and the solver's comfort level with each technique. For instance, the graphing method offers a visual representation, allowing you to literally "see" the solution as the point where the lines intersect.

To solve a system of linear equations, one must first understand what a linear equation actually entails. A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable, typically involving variables with an exponent of 1. Graphically, a linear equation represents a straight line. The solution to a system of linear equations in two variables is any ordered pair (x, y) that satisfies each equation independently. This ordered pair represents the point where the two lines intersect.

To further illustrate the concepts of systems of equations and their solutions, consider the following real-world scenarios:

• Bollyflixphd The Ultimate Guide To Streaming Bollywood Movies
• Mkvcinemas Com Old Movies Your Ultimate Destination For Retro Cinema

• Example 1: Business Planning: A company produces two products, A and B. Each product requires certain resources (labor, materials). The company has a limited amount of these resources. The equations represent the constraints: the labor hours available, the material cost limit, and the profit potential. The solution to the system of equations will help identify the optimal production quantities for each product that maximizes profit while staying within the constraints.
• Example 2: Financial Modeling: You invest in two stocks, X and Y. You have a total investment budget and a target return. Each stock has a different expected return and risk profile. The equations represent your budget constraint and your desired return. Solving the system helps determine how much to invest in each stock to meet your goals.
• Example 3: Chemical Reactions: In chemistry, equations represent chemical reactions. You might have two reactions where you need to determine the amounts of reactants needed to produce a certain amount of product.
• Example 4: Traffic Flow: In traffic management, systems of equations can model the flow of vehicles through intersections or roads. The variables could represent the number of vehicles entering and exiting certain points, and the equations would describe how traffic is distributed.

Now, let's delve deeper into the methods used for solving systems of equations.

1. Graphing Method: This method offers a visual understanding of the solution. To solve a system by graphing, each equation is plotted on the same coordinate plane. The coordinates of the point(s) where the lines intersect represent the solution(s) to the system. However, this method is less precise, particularly if the solution involves fractional or decimal values. The goal of solving systems of equations is to identify the location where the lines intersect when the equations are graphed. The (x, y) ordered pair of this intersection point is considered the solution of the system.

2. Substitution Method: The substitution method provides an algebraic approach. The core idea here is to express one variable in terms of the others using one equation, and then substituting this expression into the remaining equation(s). This process reduces the number of variables in the equation, eventually simplifying it to a single-variable equation that can be readily solved. After solving this, you substitute the known value back into any of the other original equations to solve for the other unknown. The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently.

3. Elimination Method: This method is another powerful algebraic tool. The goal is to manipulate the equations in such a way that when they are added or subtracted, one of the variables is eliminated. This typically involves multiplying one or both equations by a constant. Once a variable is eliminated, the remaining equation can be solved for the other variable. Substitute the value from step 4 into any of the other equations and solve for the other unknown. To solve the system of equations, use elimination. To solve the system of equations, use elimination.The equations are in standard form. Simplify the equations and put them in the form ax

For instance, to solve the system of equations by elimination, we use the following steps:

• Step 1: Prepare the Equations: Ensure the equations are in a standard form (ax + by = c) and aligned with the variables.
• Step 2: Match Coefficients: Identify a variable to eliminate and make its coefficients opposites in the two equations. Multiply one or both equations by a constant to achieve this. For example, to get opposite coefficients of f, multiply the top equation by -2.
• Step 3: Eliminate a Variable: Add the two equations together. This eliminates one variable, resulting in a single equation with one unknown.
• Step 4: Solve for the Remaining Variable: Solve the new equation for the remaining variable.
• Step 5: Substitute and Solve: Substitute the value obtained in Step 4 into one of the original equations to solve for the other variable. For example, Substitute s = 140 into one of the original equations and then solve for f.
• Step 6: Check the Solution: Substitute the solution (values of the variables) back into the original equations to verify that they are correct.

Each method has its own strengths. Graphing offers visual clarity, substitution is flexible for various equation forms, and elimination excels when coefficients are easily manipulated. The choice of which method to use often depends on the form of the equations and personal preference. Choosing the right method depends on how the equations are written and how comfortable the student is with each technique.

When we have several equations we are using to solve, we call the equations a system of equations. When solving a system of equations we are looking for a solution that works for all of these equations. In this discussion, we will limit ourselves to solving two equations with two unknowns.

The solution to a system of linear equations can fall into three categories:

• 1 solution: This is the most common situation and it involves lines that intersect at exactly one point. The coordinates of the points at which the two lines intersect are the solutions to the system. The \\((x, y)\\) ordered pair of this intersection point is considered the solution of the system.
• No solution: This occurs when the lines are parallel and never intersect.
• Infinite solutions: This arises when the two equations represent the same line. That is, the resulting system has the same solution set as the original system.

The system of equations can include inequalities as well, and that case needs to be solved by graphing and shading areas. \u2022 students will solve a system of inequalities graphically. \u2022 students will interpret a solution of a system of equations or inequalities in terms of the situation. \u2022 students will choose an efficient method for solving a system of equations.

Let's consolidate the information regarding the most common methods for solving systems of linear equations:

1. Substitution

• Get a variable by itself in one of the equations.
• Take the expression you got for the variable in step 1, and plug it (substitute it using parentheses) into the other equation.
• Solve the equation obtained in step 3.
• Substitute the value from step 4 into any of the other equations and solve for the other unknown.

2. Elimination

• Multiply one or both equations by a constant so that the coefficients of one variable are opposites.
• Add the equations to eliminate one variable.
• Solve the resulting equation for the remaining variable.
• Substitute the value from step 3 into either of the original equations and solve for the other variable.
• Check your solution in both of the original equations.

3. Graphing

• To solve linear simultaneous equations with two variables by graphing, plot both equations on the same set of axes.
• Determine whether the lines intersect, are parallel, or are the same line.
• The coordinates of the points at which the two lines intersect are the solutions to the system.

Solving systems of equations can seem intimidating, especially when you see more than one equation shown on a graph. However, if you know how to graph a function on the coordinate plane or on a graphing calculator, then you can become a master of solving systems of equations. And in this lesson you will learn one algebraic method for solving systems of equations, called the substitution method.

By applying these methods diligently, you will be able to confidently solve a system of equations. Remember, practice is key, and with each problem, your understanding and problem-solving abilities will strengthen, unlocking solutions to a wide range of real-world challenges.

Wolfram|alpha can also generate problems and provide feedback and guidance. Enter your equations, click calculate, and see the solution and the steps. The solve by substitution calculator allows to find the solution to a system of two or three equations in both a point form and an equation form of the answer. Click the blue arrow to submit.