Can a single graph hold the key to unlocking complex mathematical relationships? Indeed, the visual representation of a function can reveal its secrets, allowing us to decipher its equation and understand its behavior.

Deriving the function equation from a graph is a fundamental skill in mathematics, enabling us to translate visual information into algebraic expressions. The process begins with identifying the type of graph. Is it a straight line, a curve, or something more complex? Recognizing the graph's form is crucial; for instance, if the graph appears to be a straight line, we immediately check if it represents a linear function. We delve deeper into the realm of algebra, where understanding the relationship between a graph and its corresponding equation becomes paramount.

Graphing is not merely for visualization; it serves as a powerful tool for data analysis. Outliers, those points seemingly far removed from the general trend, can indicate crucial insights or skew the results of a regression equation. A keen eye for graphical representation can help identify these anomalies and their potential impact. The capacity to extract meaningful information from graphs is vital in various fields, from scientific research to financial modeling.

Let's consider a scenario where we have a sinusoidal graph. To find the equation, we first determine the midline, or the line around which the sinusoid oscillates. This is done by calculating 'd', the average of a local maximum and minimum. The midline, represented by y = d, serves as a reference point, while the amplitude, derived from the distance between the midline and the maximum or minimum, provides another key element of the equation. These elements, along with the period (the length of one complete cycle) and any phase shifts, are combined to construct the final equation.

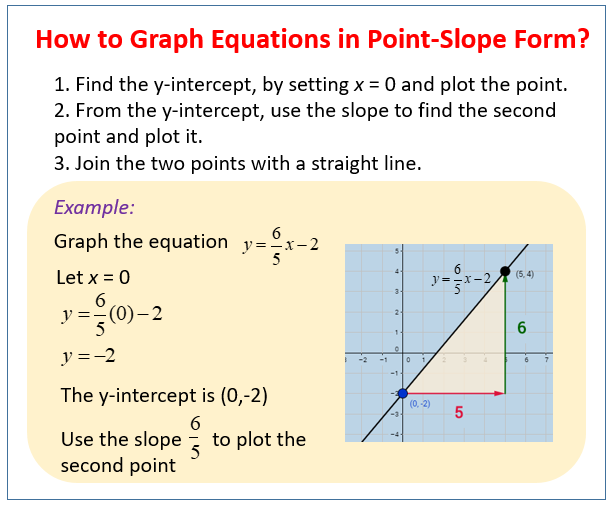
In the case of a straight-line graph, the equation takes the familiar form of \(y = mx + c\). Here, 'm' denotes the slope, indicating the rate of change, and 'c' represents the y-intercept, the point where the line crosses the y-axis. Finding the slope, 'm', requires identifying two points on the line and calculating the change in y divided by the change in x. An alternative is to find the slope from an equation by converting it into slope-intercept form; in this form, the coefficient of x is the slope. This conversion underscores the interconnectedness of graphical and algebraic representations.

The process of finding the equation from a graph involves a series of steps: first, determine the type of graph (linear, quadratic, exponential, logarithmic, etc.). Then, use the appropriate formula for that graph type, plugging in the values derived from the graph itself. For instance, if we are dealing with a circle, we use its standard equation, identifying its center and radius from the graph. This methodology allows us to translate visual features into precise mathematical expressions, solidifying our comprehension of the underlying principles.

Consider the common logarithmic function. Finding its equation requires determining its base and any horizontal or vertical shifts. The base can be determined if we know one point on the graph. The graph \(y = log_b(x)\) passes through (1, 0). If the curve has been shifted, identifying the horizontal asymptote helps us find the vertical translation and, subsequently, the value of k in the equation. This methodical procedure is adaptable to many situations, demonstrating its flexibility and power.

The equation of a sine or cosine graph offers another example. The graph is described by functions of the form \(y = A sin(Bx + C) + D\), with A being the amplitude, B affecting the period, C affecting the phase shift, and D the vertical shift or midline. By examining these parameters on the graph, we can fully define the corresponding equation, demonstrating once again how information is extracted from a graph and translated into the correct formula.

Beyond single functions, graphs provide essential tools for evaluating multiple relationships simultaneously. For example, graphing proportional relationships allows us to interpret the unit rate as the slope. Comparing two such relationships graphically offers a clear method for comparing their rates of change, offering valuable insight into their properties.

Let's consider a specific example: finding the equation of a line given two points. The steps here involve calculating the slope using the coordinates of the two points, and then using the point-slope form of a linear equation. Alternative methods and multiple examples demonstrate the flexibility of the approach.

Many tools, such as free graphing calculators, are available to aid in this process, allowing users to instantly graph math problems, and aiding in visualization. Mathway, for example, allows users to graph a wide range of equations, supporting the understanding of mathematical concepts through visualization. These tools are invaluable for both learning and practicing the concepts. They are able to handle multiple variables, solve systems of equations, and also help with visualizing the equations.

Here's a table summarizing the main concepts:

Concept	Description	Key Steps	Example
Linear Functions	Functions that produce a straight-line graph.	1. Identify two points on the line. 2. Calculate the slope (m). 3. Find the y-intercept (c). 4. Use the equation \(y = mx + c\)	Given points (1, 2) and (3, 6), m = (6-2)/(3-1) = 2. If \(c=0\), the equation is \(y=2x\)
Sinusoidal Functions	Functions like sine and cosine, which have wave-like graphs.	1. Find the midline (d). 2. Find the amplitude (A). 3. Determine the period. 4. Determine any phase shift. 5. Use the formula: \(y = A sin(Bx + C) + D\)	For a sine wave with a midline at y=2, an amplitude of 3, and a period of 2, the equation is \(y=3sin(x)+2\).
Logarithmic Functions	Functions of the form \(y = log_b(x)\).	1. Identify a point (x, y) on the graph. 2. Assume no horizontal shifts (initially). 3. Use the point to find the base (b).	If a graph passes through (12, 2.5), and \(y = log_b(x)\), solve for b: 2.5 = log_b(12).
Circles	Geometric shapes that are round.	1. Identify the center (h, k) and radius (r) from the graph. 2. Use the equation \((x - h)^2 + (y - k)^2 = r^2\)	If the center is (2, 3) and radius is 4, the equation is \((x - 2)^2 + (y - 3)^2 = 16\)
Finding Slope	Determining the rate of change of a line.	1. Identify two points on the line. 2. Calculate the change in y divided by the change in x (rise over run).	For points (1, 2) and (3, 6), slope = (6-2)/(3-1) = 2.