Do you ever find yourself grappling with the abstract world of mathematics, particularly when it comes to visualizing relationships between variables? Understanding linear graphs is not just a fundamental concept in mathematics; it's a crucial skill for interpreting data and making informed decisions in various aspects of life.
A linear graph, at its core, is a visual representation of a linear equation. This equation describes a relationship between two variables where the highest power of the variable is one. The resulting graph is, predictably, a straight line. This simplicity, however, belies its power. Linear graphs are used extensively in fields ranging from economics and finance to physics and engineering, offering a clear and concise way to understand trends and patterns.
Before we delve deeper, let's clarify a common point of confusion: the distinction between linear graphs and line graphs. While they sound similar, they represent different concepts. A linear graph is a straight line representing a linear equation. A line graph, on the other hand, is a broader term that can encompass any graph where data points are connected by line segments. This means all linear graphs are line graphs, but not all line graphs are linear graphs. Think of it like this: all squares are rectangles, but not all rectangles are squares.
- Aagmal Given The Ultimate Guide To Unlocking Its Potential
- Unlock The Power Of My Deshico Your Ultimate Guide To Online Learning And Beyond
The fundamental equation governing linear graphs is the slope-intercept form: Y = mx + c. This equation, though seemingly simple, unlocks the secrets of linear relationships. Let's break down its components:
- 'Y' represents the dependent variable, whose value changes in response to changes in the independent variable.
- 'x' represents the independent variable, whose value can be freely chosen or altered.
- 'm' represents the slope of the line, indicating the rate of change of the dependent variable with respect to the independent variable. A positive slope means the line slopes upwards from left to right, a negative slope means it slopes downwards, and a slope of zero indicates a horizontal line.
- 'c' represents the y-intercept, which is the point where the line intersects the y-axis (where x = 0).
To illustrate these concepts, consider an example: "7x + y = 8." This is a linear equation in the standard form. To visualize it, we can rearrange it to the slope-intercept form: y = -7x + 8. In this equation, the slope (m) is -7, and the y-intercept (c) is 8. The graph of this equation would be a straight line with a negative slope, intersecting the y-axis at the point (0, 8).
There are several methods to unravel and work with linear equations. Four common techniques for solving a system of linear equations include graphing, substitution, elimination, and using matrices. The selection of the most suitable method often relies on the nature of the equations and the desired level of precision.
- Hdhub4u 18 Unveiling The World Of Premium Content
- Filmy Fly Stream Your Ultimate Guide To Seamless Movie Streaming
| Concept | Description |
|---|---|
| Linear Equation | An algebraic equation in which the highest power of the variable is 1. It forms a straight line when graphed. |
| Linear Graph | A straight line that represents a linear relationship between two variables. It is the visual representation of a linear equation. |
| Slope (m) | Indicates the rate of change of the dependent variable (y) with respect to the independent variable (x). It dictates the steepness and direction of the line. |
| Y-intercept (c) | The point where the line intersects the y-axis (where x=0). It is the value of y when x is zero. |
| Standard Form of a Linear Equation | Generally expressed as Ax + By = C, where A, B, and C are constants. |
| Slope-Intercept Form of a Linear Equation | Generally expressed as y = mx + c, where 'm' is the slope and 'c' is the y-intercept. |
| Collinear Points | Points that lie on the same straight line. |
Let's delve deeper into the mechanics of constructing these visual representations. Plotting a linear graph often involves following these fundamental steps:
- Ensure the Equation is in Slope-Intercept Form: This form (y = mx + c) makes identifying the slope and y-intercept straightforward.
- Identify the Slope (m) and Y-intercept (c): Once the equation is in slope-intercept form, these values are readily apparent.
- Plot the Y-intercept: This is the point (0, c) where the line crosses the y-axis.
- Use the Slope to Find Another Point: The slope (m) represents the "rise over run." Convert the 'm' value into a fraction. For example, if the slope is 2 (or 2/1), from the y-intercept, go up 2 units (rise) and right 1 unit (run). Plot this second point.
- Draw a Straight Line: Connect the y-intercept and the second point with a straight line. Extend the line in both directions, indicating that it continues infinitely.
Consider the example of graphing the equation y = 2x + 1. The y-intercept is 1, so plot the point (0, 1). The slope is 2 (or 2/1). From the point (0, 1), go up 2 units and right 1 unit, plotting the point (1, 3). Draw a straight line through these two points to create the graph of this equation.
Line graphs are incredibly versatile. They are often used in fields such as finance to represent stock market performance over time or in scientific research to chart the relationship between variables in experiments. They help visualize trends and patterns and they enable a deeper understanding of the changes happening over a period.
Now, let's examine a slightly different application of this knowledge: understanding systems of linear equations. Sometimes, you may encounter multiple linear equations simultaneously. This is called a system of linear equations. Graphing these systems involves plotting each equation on the same coordinate plane. The point(s) where the lines intersect represent the solution(s) to the system. If the lines are parallel, there is no solution, indicating that the system of equations is inconsistent. If the lines are coincident (overlapping), there are infinitely many solutions.
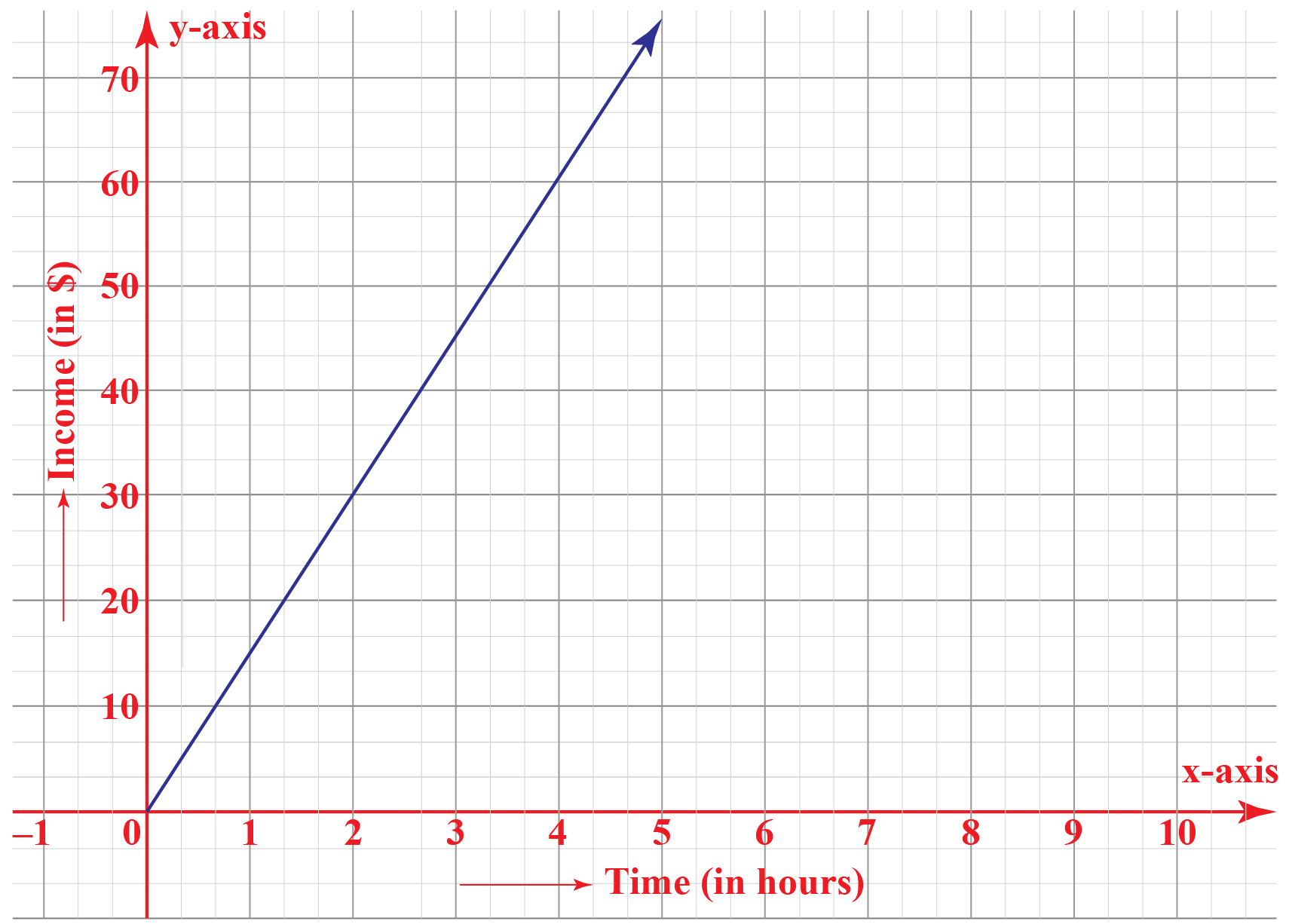
To grasp this concept fully, let's consider a practical example. Suppose we have a pay-as-you-go phone plan. The cost is represented by an equation y = mx + c, with the equation y = 5x + 4, where 'x' represents the number of minutes used and 'y' represents the total cost. In this equation, the slope (m) is 5, and the y-intercept (c) is 4. If 'x' equals 4, this means 4 minutes is used, and the y-value is what we are looking for, this indicates the total cost of the 4 minutes. The equation for the cost would be y = 5(4) + 4, making the total cost y = 24. Thus, the cost for 4 minutes is 24.
Beyond this, we also have line graphs, which can be used to represent quantitative data collected over a specific subject and a specific time interval. In these graphs, all data points are connected by a line, providing a clear visual representation of trends and changes over time. They enable easy analysis of data collected over a specific period. This enables us to quickly identify trends.
To solidify your understanding, remember that a linear graph is a straight line, and it always will be. A line graph however, does not have to be, and can use line segments or a single line to connect data points. The word "linear" itself comes from "line," a simple mnemonic device to aid recall.
In summary, understanding linear graphs is essential. Their applications span a wide range of disciplines, making this a truly valuable skill. With practice and understanding of the key concepts, you will find that the world of linear graphs will begin to unfold a world of insightful representations that transform complex data into easily digestible understanding.
- Bollywood Movies And Bollyflix Your Ultimate Guide To The World Of Indian Cinema
- Tamilblazers Re Your Ultimate Guide To Understanding The Trend