Can a single line truly unlock the secrets of a shape, revealing its hidden balance and mirroring its very essence? The axis of symmetry, often overlooked, is the key to understanding geometric harmony and the predictable behavior of mathematical functions.

Delving into the realm of geometry, the axis of symmetry emerges as a fundamental concept, a straight line acting as a mirror within a shape. It's the invisible spine around which a figure's perfect balance is achieved, ensuring that every point on one side finds its identical twin on the other. This concept is not merely a geometric curiosity; it's a powerful tool for understanding symmetry, and, through it, the underlying structure of everything from simple squares to the complex curves of parabolas. The axis of symmetry is also known as the line of symmetry, the symmetrical axis that creates a mirror image like the reflection on each side of the parabola.

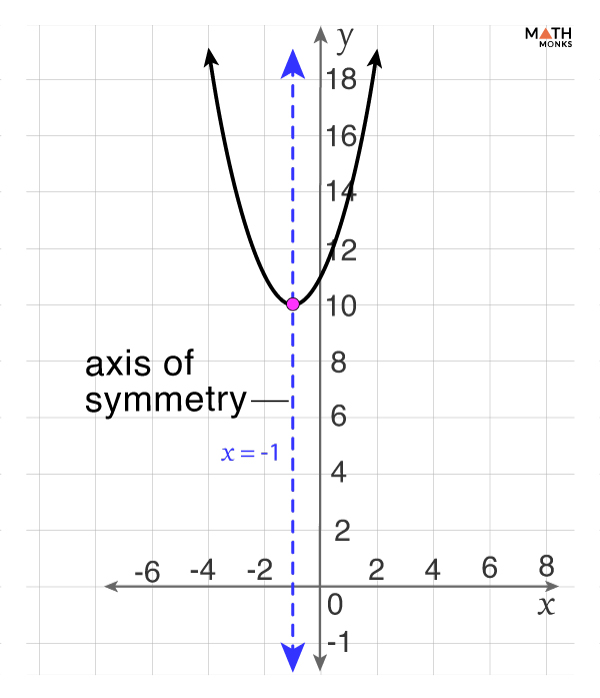
The axis of symmetry is a fundamental concept in understanding the properties of parabolas, which are the U-shaped curves that represent quadratic functions. Every parabola is divided into two congruent halves by its axis of symmetry. This line is always a vertical line that runs through the vertex of the parabola. The vertex is the point where the parabola changes direction, representing either its highest or lowest point. The axis of symmetry is not the same as the vertex, but it passes through it. Identification of the vertex helps us to calculate the position of the axis of symmetry. The axis of symmetry always passes through the vertex of the parabola.

For example, consider a parabola defined by the quadratic function. The vertex is a crucial point on the parabola. The axis of symmetry is a vertical line that passes through the vertex. If the vertex is located at the point (1, 2), then the axis of symmetry is the vertical line x = 1. This is because the axis of symmetry is always parallel to the y-axis and passes through the x-coordinate of the vertex. If we know the vertex is at the point (1, 2), this tells us that the axis of symmetry is also at 1. The vertical line drawn at x=1 is the axis of symmetry. This means that if we know a point on one side of the parabola we will also know a point on the other side based on the axis of symmetry. The axis of symmetry corresponds to the symmetric line for the graph of quadratic function, which is a parabola.

The quadratic equation of a parabola is generally represented in the form y = ax + bx + c, where a, b, and c are constants. The equation can be used to find the axis of symmetry for any parabola. The formula to calculate the axis of symmetry for a parabola equation is also available.

Now, lets explore how the axis of symmetry is derived. To derive the axis of symmetry for a parabola, we start with the quadratic function y = ax + bx + c. Completing the square, we rewrite the equation in vertex form. This form highlights the vertex of the parabola. The x-coordinate of the vertex, and thus the axis of symmetry, can be found using the formula x = -b / 2a. This equation provides a direct means of determining the axis of symmetry from the coefficients of the quadratic function. So, having a reference for the symmetry gives a lot of information about the parabola. For example, the roots of the equation will be disposed symmetrically with respect to this axis of symmetry.

Understanding symmetry isn't confined to static shapes. It also applies to mathematical functions, particularly quadratic equations, which take the form y = ax + bx + c. This equation is fundamental in algebra and is used to graph parabolas. The axis of symmetry is crucial here because it divides the parabola into two congruent halves, mirroring one side onto the other. This property allows us to predict the behavior of the function across its entire domain. By knowing the axis of symmetry, the vertex, and a few key points, we can easily sketch the entire graph of a quadratic function. Learn how to find the axis of symmetry of a parabola from its equation or from its graph. Use formulas, interactive applet, examples and practice problems to master this concept.

The concept of symmetry is also crucial in understanding the transformations of graphs. We can reflect the graph of a function across the axis of symmetry to create a mirror image. This reflection doesn't alter the fundamental characteristics of the shape but simply changes its orientation. For example, plotting the mirror images of points across the axis of symmetry will provide the correct shape.

The axis of symmetry also becomes important in solving quadratic equations. The roots (or x-intercepts) of a quadratic equation are located symmetrically around the axis of symmetry. This symmetry allows us to find the roots or verify their accuracy. The axis of symmetry is the line that passes through the vertex and is perpendicular to the directrix. Remember, when drawing the parabola to avoid connecting the dots with straight line segments.

The concept of symmetry also extends beyond parabolas. Regular polygons, like squares, rectangles, and circles, also exhibit symmetry, each with a unique number of axes of symmetry. A square has 4 lines of symmetry, a rectangle has 2 lines of symmetry, and a circle has infinite lines of symmetry. On the other hand, a parallelogram has no line of symmetry. Understanding these differences is key to recognizing and classifying geometric shapes. For example, a regular polygon with n sides has n axes of symmetry.

The axis of symmetry can be either vertical, horizontal, or diagonal. To find the axis of symmetry of a shape, you need to know the coordinates of the vertices (the corners) of the shape. The axis of symmetry is a straight line that makes the shape of the object symmetrical. It creates precise reflections on each of its sides. If we fold and unfold an object along the axis of symmetry, its two sides are the same. The axis of symmetry can be a straight line that makes the shape of the object symmetrical. Therefore, the axis of symmetry is x = 3. And the axis of symmetry is a vertical line.

Consider the graph of a quadratic function. This algebra math tutorial explains how to find the vertex and the axis of symmetry of a parabola from quadratic functions given in standard form, vertex for.

Understanding the axis of symmetry is more than just an exercise in mathematics; it's a fundamental skill for anyone who wants to understand the world around them. Symmetry is all around us, from the shapes of natural objects to the designs of man-made structures. By learning about the axis of symmetry, we can appreciate the beauty and order that symmetry brings to our world. This line helps us understand symmetry and the behavior of mathematical functions and shapes. A parabolas axis of symmetry is a vertical line through the vertex. Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Remember, when drawing the parabola to avoid connecting the dots with straight line segments. This video explains what the axis of symmetry is, what the formula is

The axis of symmetry is best studied in a parabola, while graphing a quadratic function. Let us derive the equation of the axis of symmetry. The symmetrical axis is also known as the line of symmetry that creates a mirror image like the reflection on each side of the parabola. The axis of symmetry of this parabola will be the line x = -b/2a. The axis of symmetry always passes through the vertex of the parabola. Thus identification of the vertex helps us to calculate the position of the axis of symmetry. The quadratic equation of a parabola is, y = ax + bx + c (up/down parabola).

Here's a table that helps summarize the key concepts and applications of the axis of symmetry, which is a core element in understanding various mathematical and geometric concepts, with focus on parabolas:

Concept	Description	Application/Significance
Definition	A straight line that divides a shape into two congruent halves, creating a mirror image.	Essential for understanding symmetry and the behavior of geometric shapes and mathematical functions.
Parabola	The axis of symmetry is a vertical line that passes through the vertex of the parabola.	Crucial for graphing quadratic functions, finding the vertex, and determining the roots of the equation.
Vertex	The point on the parabola where it changes direction (highest or lowest point).	The axis of symmetry always passes through the vertex.
Quadratic Equations	Equations in the form y = ax + bx + c.	The axis of symmetry helps determine the graph's symmetry and the roots of the equation.
Formula for Axis of Symmetry	x = -b / 2a (derived from the quadratic formula).	Allows for a direct calculation of the axis of symmetry from the equation's coefficients.
Geometric Shapes	Shapes like squares, rectangles, and circles.	Each shape has its own number of axes of symmetry, crucial for classification and understanding.
Transformations	Reflecting a graph across the axis of symmetry.	Understanding transformations and manipulations of the graph of functions.
Roots of an Equation	Points where the graph intersects the x-axis.	The roots of a quadratic equation are symmetrically located around the axis of symmetry.