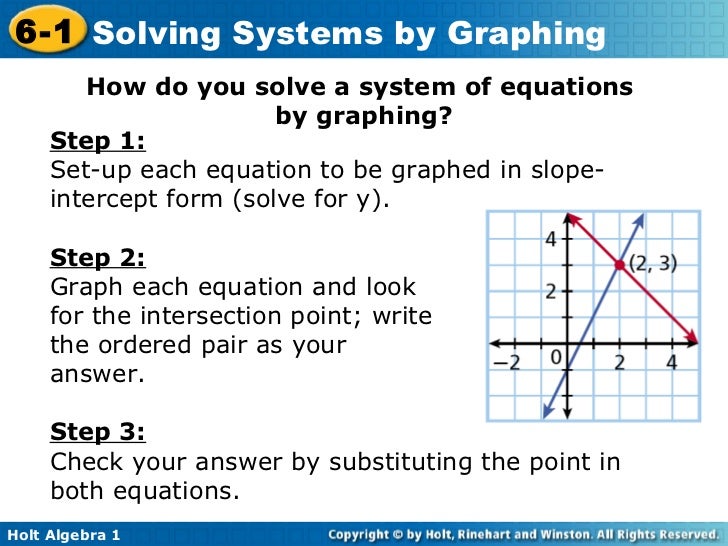
Can you truly visualize the solution to a mathematical puzzle? Solving systems of equations by graphing unlocks a visual pathway to understanding, transforming abstract algebra into a concrete, intuitive process.

At the heart of mathematics lies the elegance of solving equations, and among the diverse methods available, solving systems of equations by graphing stands out for its visual clarity. This approach allows us to translate abstract algebraic relationships into tangible geometric representations, providing a unique lens through which to understand and solve problems. While other methods, such as substitution or elimination, offer algebraic solutions, graphing offers a graphical insight, transforming equations into lines and their solutions into points of intersection.

Consider the simple equation: x + y = 7. This represents an infinite number of solutions, pairs of x and y values that, when added together, equal seven. Graphing allows us to visualize this infinity as a single line, with every point on the line representing a valid solution. By introducing a second equation, such as X + 3y = 0, we create a system, seeking a single solution - a point that satisfies both equations. The graph, then, becomes our guide to this shared solution: the point where the two lines intersect.

The power of graphing lies not just in finding the answer, but in understanding the nature of the system itself. Is there one solution, no solution, or infinitely many? The visual representation provides an immediate answer. Parallel lines? No solution. Coincident lines (overlapping each other)? Infinite solutions. Intersecting lines? One unique solution.

This method, far from being merely a supplementary technique, offers a fundamental understanding of the relationships between equations and their solutions. It provides a way to interpret graphs to identify solutions, offering an intuitive method, applicable even beyond linear systems, albeit requiring a deeper understanding of the curves involved.

Solving systems of equations by graphing, therefore, is more than just a technique; it's a visual gateway to the core concepts of algebra. It allows you to see, to understand, and to solve, all within a single glance at a graph.

The process is generally laid out in several clear steps:

Graph Each Equation: The initial step involves plotting each equation on the same coordinate plane. If you're working with linear equations, this means drawing two straight lines. For each line, identify the slope and y-intercept, allowing you to draw it accurately.
Estimate the Point of Intersection: Once both equations are graphed, the next step is to visually identify where the lines intersect. This point represents the potential solution to the system of equations.
Check the Solution: To ensure accuracy, substitute the x and y values of the estimated intersection point into both of the original equations. If both equations hold true, then the point is indeed the solution.

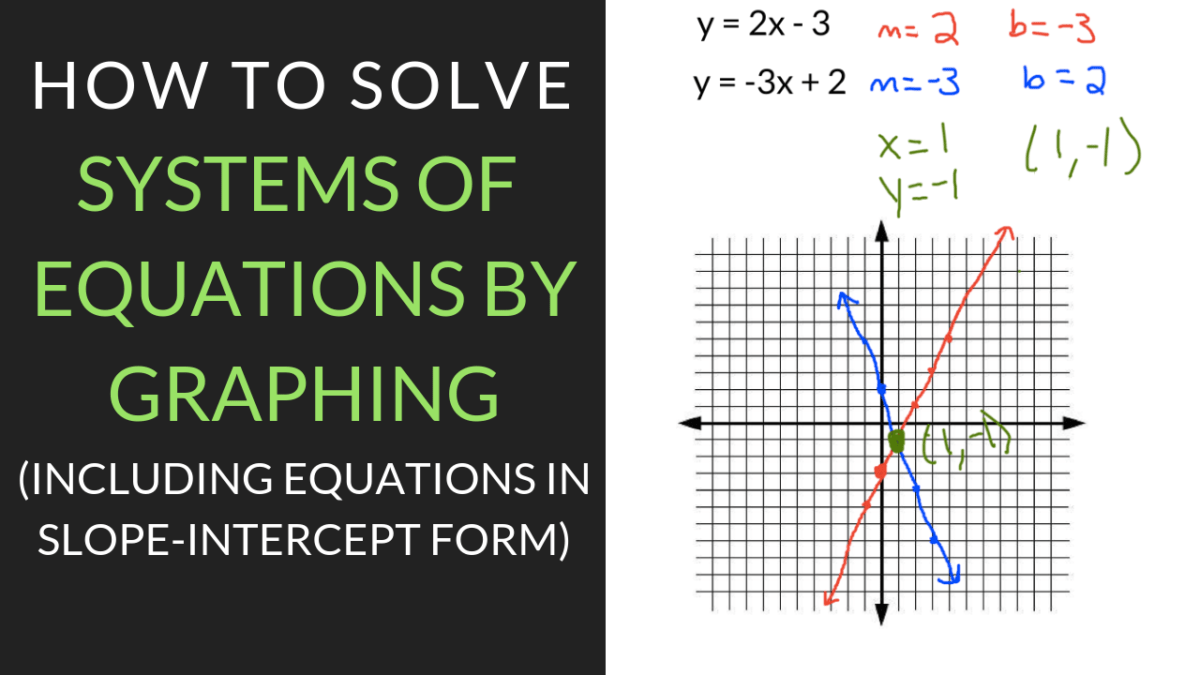
For instance, let's consider solving the system:

x + y = 7
x - y = 1

First, graph both equations. The first equation (x + y = 7) can be rewritten in slope-intercept form as y = -x + 7. This means the line has a y-intercept of 7 and a slope of -1 (meaning for every one unit increase in x, y decreases by one unit). The second equation (x - y = 1) can be rewritten as y = x - 1. This has a y-intercept of -1 and a slope of 1. Graph these two lines on the same coordinate plane.

Visually, the lines intersect at the point (4, 3). Step 3 requires substituting those values into the original equations:

For x + y = 7: 4 + 3 = 7. The equation is true.
For x - y = 1: 4 - 3 = 1. The equation is true.

Since the point (4, 3) satisfies both equations, it is indeed the solution to the system.

In more advanced cases, you may encounter non-linear equations, like a parabola and a line, or a circle and a line. The principles remain the same: graph the equations and find the point(s) of intersection.

Consider the intersection between a line and a parabola. In these cases, there may be two points of intersection, one, or none depending on the equations and how they intersect.

Solving systems of equations by graphing offers a tangible method that complements more complex techniques. By visually representing the relationships between equations, you can see the solutions directly. By the time students reach 8th grade, they're already familiar with linear systems. However, the ability to grasp these systems with clarity is a valuable skill.

The ability to determine whether an ordered pair is a solution of a system of equations; and to solve a system of linear equations by graphing, are critical skills that can be gained by the end of a detailed study of these concepts.

The process of graphing is facilitated by tools, from pencil and paper to advanced graphing calculators. Graphical solutions, especially using a graphing calculator, are quick methods for finding a solution, allowing you to approximate the solution. Whether by hand or with technology, the objective remains the same, find the intersections, confirm the solutions.

However, graphing can be more challenging when dealing with equations that are difficult to rearrange into slope-intercept form or those that involve large or non-integer coefficients. In these cases, more algebraic methods like substitution or elimination may be more efficient.

The type of system is described by how the lines interact with each other when graphed. These interactions help us categorize and understand the characteristics of the system:

Consistent and Independent: This is the most common type. The lines intersect at a single point, representing a unique solution.
Consistent and Dependent: The equations are equivalent, resulting in lines that lie directly on top of each other (coincident lines). They have infinite solutions, and any point on the line is a solution to the system.
Inconsistent: The lines are parallel and never intersect. Therefore, the system has no solution.

For example, in a system of equations where the two equations are essentially the same, the system is considered dependent. For instance, if the two equations in a dependent system reduced down to y = -x + 3, then you should state the solution as being that line equation.

A system's solution is the intersection of its lines. The key is to find the point (or points) that satisfy all the equations in the system. This approach underscores the relationship between the graphical representation and the solutions of the system.

In essence, solving systems of equations by graphing provides an intuitive approach to understanding and solving these important algebraic challenges.

Consider the steps to solve a linear system by graphing:

Write each equation in slope-intercept form, which is y = mx + b. (where m is the slope and b is the y-intercept)
Use the y-intercept and slope to plot the first line.
Use the y-intercept and slope to plot the second line on the same grid.
Find the point of intersection.
Check the solution to the system by substituting the x and y values from the point of intersection into both of the original equations.

The method is an excellent way to grasp the core concepts of algebra, providing a crucial visual connection between equations and their solutions.

There are several strategies for solving systems of equations. The approach you select depends on the equations in your system and the level of precision required for the solution. While we explored the graphing method in detail here, other strategies include:

Substitution: Substitute one equation's expression for a variable into the other equation, reducing the system to a single variable equation.
Elimination: Manipulate the equations (often by multiplying them by constants) so that either the x or y variable is eliminated when the equations are added or subtracted.

Each approach has its own advantages and disadvantages. While graphing provides the most visual approach, substitution and elimination tend to be more efficient for complex equations.

Students first encounter solving systems of equations in the 8th grade when they study linear systems. Graphical solutions, especially using a graphing calculator, are quick methods for finding a solution, allowing you to approximate the solution. To solve a system of linear equations by graphing, which are systems made up of two linear equations, first, make sure that you have two linear equations, or equations that form lines when graphed.

In conclusion, the art of graphing in algebra is very useful.